Спектры манипулированных сигналов

2.5.1. Амплитудная манипуляция. При амплитудной манипуляции (см. рис.4.14) огибающая повторяет форму первичного сигнала, т.е. получаются гармонические колебания, амплитуда которых имеет два значения: 2U₀ и 0. Следовательно, U_max=U₀(1+m) и U_min=U₀(1-m).

Рис.4.14

Если спектр модулирующего сигнала известен, то нетрудно построить спектр сигнала после амплитудной манипуляции по правилу [14]:

- сместить спектр модулирующего сигнала на интервал частот, равный несущей частоте;

- спектр зеркально отобразить относительно спектральной линии на несущей частоте.

2.5.2. Частотная манипуляция. При частотной манипуляции (см. рис.4.15) сигнал можно представить как сумму двух сигналов U₁ и U₂ с амплитудной модуляцией. Спектр сигнала при частотной манипуляции состоит из спектров двух амплитудно-модулированных сигналов.

Рис.4.15

2.5.3. Фазовая манипуляция. Если рассматривается манипулирование по фазе на 180°, то спектр данной фазовой манипуляции находится из спектра сигнала при амплитудной манипуляции последовательностью двоичных двуполярных импульсов (см. рис.4.16).

Если к сигналу U₀(t) (часть б рис.4.16) добавить немодулированное несущее колебание U₀(t) той же амплитуды (часть в рис.4.16) и частоты, то получим амплитудно-модулированный сигнал с двойной амплитудой U₀ (часть г рис.4.16). Следовательно, спектр сигнала при манипуляции по фазе можно получить из спектра АМ-сигнала (см. часть а рис.4.16), увеличив вдвое амплитуды всех боковых составляющих и исключив колебания несущей частоты (см. часть б рис.4.16).

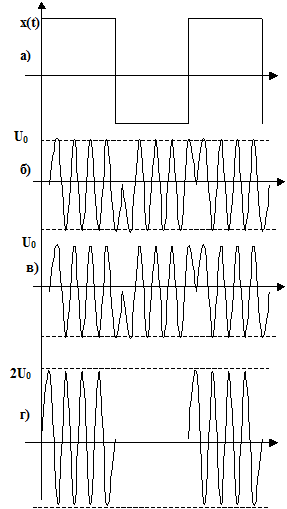
Рис.4.16

Однако на приемнике фаза принимаемого сигнала не известна и не может быть однозначно установлена. Поэтому применяется относительная фазовая манипуляция (ОФМ), при которой манипуляция фазы происходит относительно фазы предшествующей посылки. Т.е. скачок фазы имеет место тогда, когда в кодовой комбинации повторяются один за другим импульсы или паузы.

Получение спектра фазоманипулированного сигнала из спектра амплитудоманипулированного сигнала показано на рис. 4.17.

Рис.4.17

Дата добавления: 2015-10-21