
Читайте также:
|
Рассмотрим влияние шумов на ортогональность двух сигналов. В качестве входного сигнала будем использовать уже использованный в предыдущем пункте исследования гармонический сигнал s1(t) с частотой f=27 кГц. Положим n(t) – сигнал с генератора шумов. Рассмотрим ортогональность сигналов s1(t)+n(t) и s1(t).
Скалярное произведение сигналов s1(t)+n(t) и s1(t) изображено на рис.16.

Рис.16. Осциллограмма скалярного произведения сигналов s1(t)+n(t) и s1(t).
Отключим сигнал с генератора шумов. Получим скалярное произведение сигнала s1(t) на самого себя, осциллограмму которого мы уже наблюдали (см. рис.10):

Рис.17. Скалярное произведение сигнала s1(t) на самого себя.
Сравнивая осциллограммы на рис. 16 и на рис.17, можно сделать вывод, что влияние шума на величину скалярного произведения незначительно. Соответственно логично предположить, что при отключении от сумматора сигнала s1(t) скалярное произведение n(t) и s1(t) будет равно нулю. Осциллограмма на рис.18 подтверждает наше предположение.

Рис.18. Скалярное произведение сигналов s1(t) и n(t).
Данное явление можно объяснить тем, что значения функции n(t), возможно, равномерно распределены на некотором отрезке, и в разложении n(t) в ряд Фурье основной вклад в построение n(t) вносит только главная гармоника, значение частоты которой имеет со значением частоты сигнала s1(t) наибольший общий делитель, не равный 1. То есть в некотором приближении функцию n(t) можно заменить гармонической функцией, ортогональной s1(t).
Рассмотрим скалярное произведение двух гармонических сигналов (s1(t) и сигнал с частотой 27 кГц от встроенного ЗГ). На рис.19 изображено скалярное произведение этих сигналов.
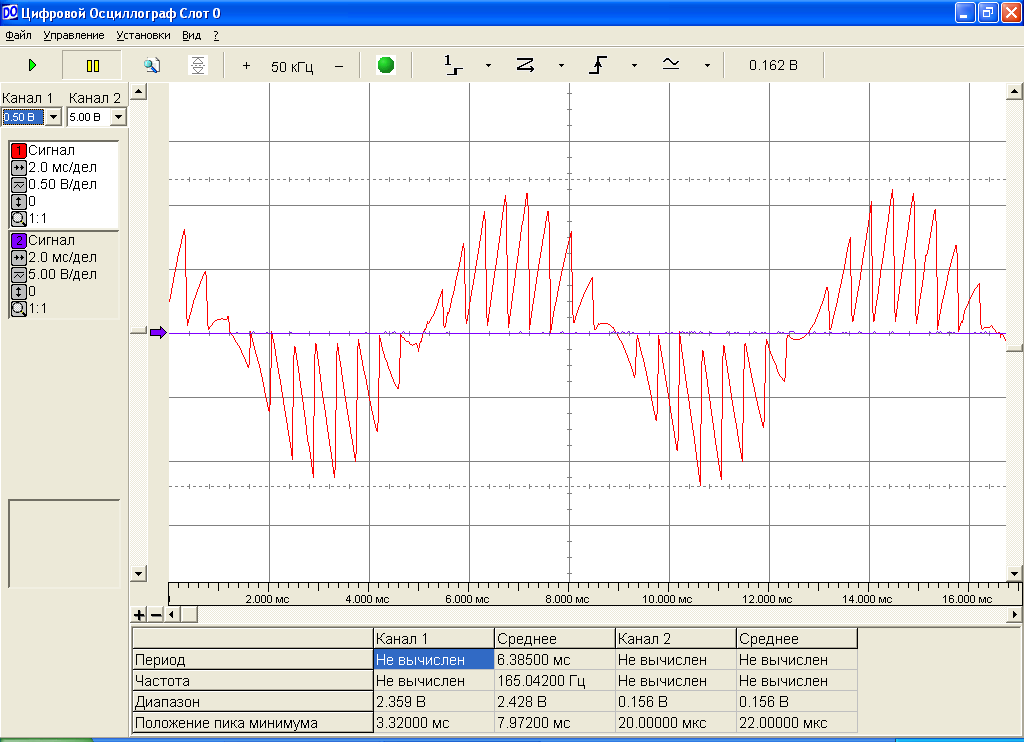
Рис.19. Скалярное произведение s1(t) и сигнала от встроенного ЗГ.
Поскольку скалярное произведение меняет свой знак (исходя из рис.19), а исходные сигналы имеют одинаковую частоту, то можно сделать вывод, что исходные сигналы отличаются по фазе.
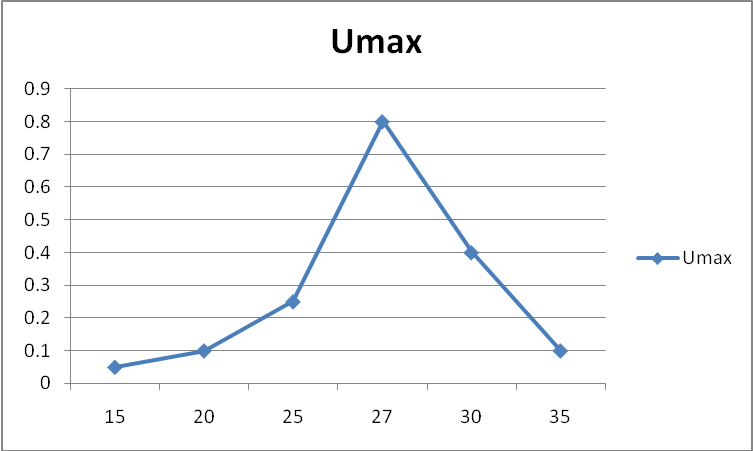
| fЗГ | кГц | |||||
| Umax | Дел | 0.05 | 0.1 | 0.25 | 0.4 | 0.1 |
Дата добавления: 2015-10-21; просмотров: 235 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Исследование ортогональности гармонических сигналов при частотной модуляции. | | | Передача дискретных сигналов через канал без помех |