Исследование ортогональности гармонических сигналов при частотной модуляции.

Государственное образовательное учреждение высшего профессионального образования

Ульяновский государственный университет.

Факультет Математики и информационных технологий

Кафедра Телекоммуникационных технологий и сетей.

Лабораторная работа №19

по дисциплине:

«Основы передачи дискретных данных»

Тема:

«Исследование свойств ортогональности гармонических сигналов»

Выполнили:

Вислов К.

Звягинцева Е.

Никонов Н.

Косян П.

Козлов Д.

Дуницына С.

Камалтдинов Д.

Крапивцев И.

Минеев Е.

Студенты гр. ИС-О-09/1

Ульяновск 2012г.

Цель работы

Экспериментальное исследование условия, при которых обеспечивается ортогональность гармонических сигналов.

Задание.

Исследование ортогональности гармонических сигналов с различными частотными и фазовыми соотношениями.

Исследование ортогональности гармонических сигналов при частотной модуляции.

В данном пункте исследования будет рассмотрена ортогональность двух гармонических сигналов s0(t) и s1(t) с частотами f1=18 кГц и f2=27 кГц.

На вход демодулятора подадим сигнал s0(t) со входа модулятора.

Осциллограмма сигнала s0(t) изображена на рис.1.

Рис.1. Осциллограмма сигнала s0(t)

Проверим ортогональность двух одинаковых сигналов s0(t), а также сигналов s0(t) и s1(t). Для этого сначала определим формы соответствующих произведений сигналов, а затем определим скалярное произведение результирующих сигналов. Если окажется, что скалярное произведение равно нулю на отрезке [0;T], где T=450 мкс (длительность символа), то соответствующие исходные сигналы являются ортогональными.

Осциллограммы произведения сигналов s0(t)*s0(t) и s0(t)*s1(t) приведены на рис.2 и рис.3

Рис.2. Осциллограмма произведения двух сигналов s0(t).

Рис.3. Осциллограмма произведения сигналов s0(t) и s1(t).

На рис.4 приведена осциллограмма скалярного произведения сигнала s0(t) на самого себя.

Рис.4. Осциллограмма скалярного произведения сигнала s0(t) на самого себя.

Исходя из рис.4 можно сделать вывод, что сигнал s0(t) не ортогонален самому себе, так как скалярное произведение за период не равно нулю.

На рис.5 изображена осциллограмма скалярного произведения сигналов s0(t) и s1(t).

Рис.5. Скалярное произведение сигналов s1(t) и s0(t).

С учетом помех в системе связи можно сделать вывод, что сигналы s1(t) и s0(t) являются ортогональными.

Теперь на вход демодулятора подадим сигнал s1(t) с входа модулятора. Осциллограмма сигнала s1(t) изображена на рис.6.

Рис.6. Осциллограмма сигнала s1(t).

Фиксируя произведение сигналов s0(t) и s1(t) на верхнем перемножителе (рис.7), получим тот же сигнал, что и на рис.3, поскольку операция умножения обладает свойством коммутативности.

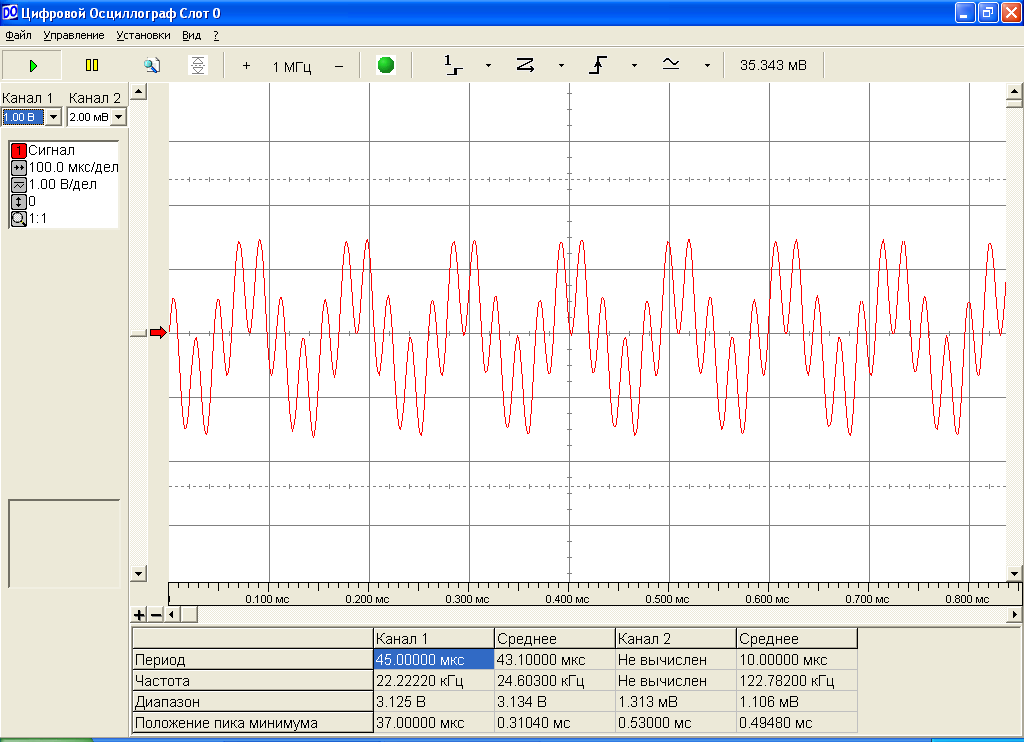
Рис.7. Осциллограмма произведения сигналов s0(t) и s1(t).

Осциллограмма произведения сигнала s1(t) на самого себя изображена на рис.8. При перемножении сигнала на самого себя его частота увеличивается в 2 раза, таким образом, частота сигнала, изображенного на рис.8, составляет 54 кГц.

Рис.8. Осциллограмма произведения двух сигналов s1(t).

Мы уже определили (см. вывод после рис.5), что сигналы s1(t) и s0(t) являются ортогональными. В данном случае мы по сути переставили местами множители скалярного произведения (в случае с рис.5 на вход подавался сигнал s0(t) и перемножался с сигналом s1(t) (нижний перемножитель), сейчас же на вход подан сигнал s1(t) и перемножается с сигналом s0(t) (верхний перемножитель)), что не меняет значение скалярного произведения.

На рис.9 изображена осциллограмма скалярного произведения сигналов s0(t) и s1(t).

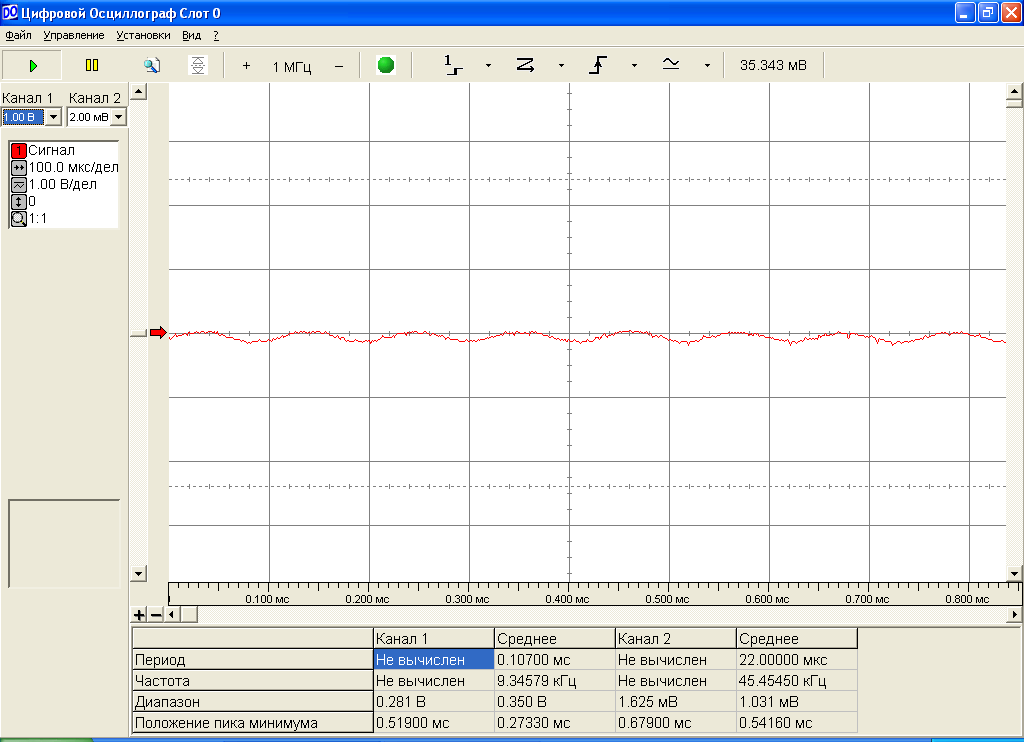
Рис.9. Скалярное произведение сигналов s1(t) и s0(t).

Скалярное произведение сигнала s1(t) на самого себя показано на рис.10.

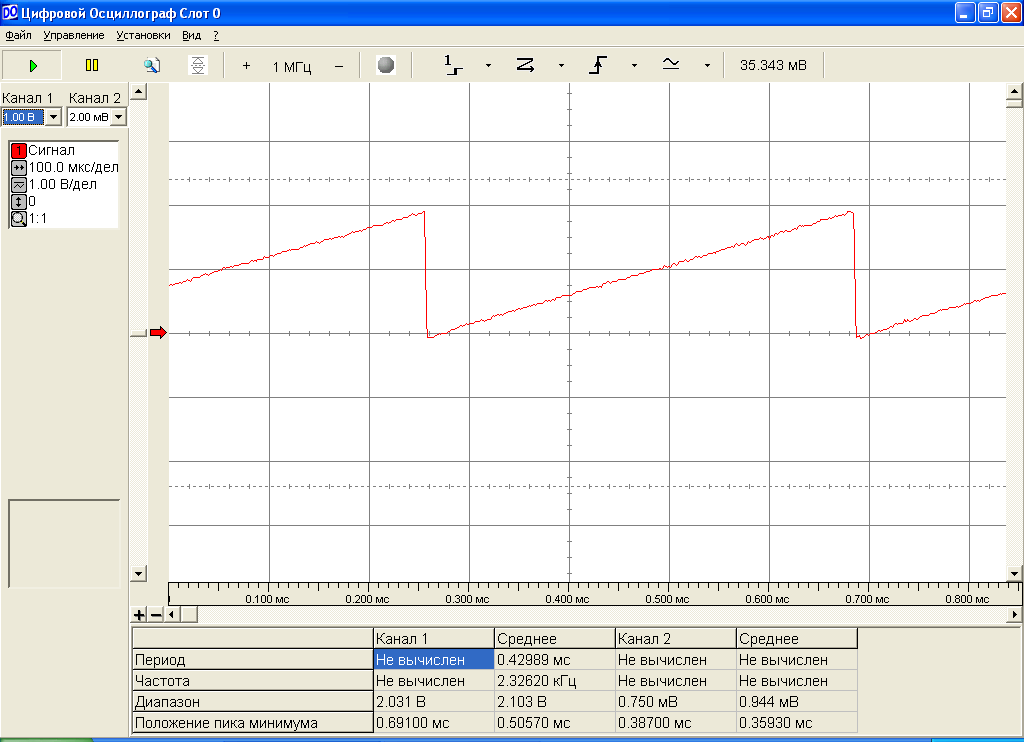
Рис.10. Скалярное произведение сигнала s1(t) на самого себя.

Скалярное произведение за период не равно нулю, сигнал s1(t) не является ортогональным по отношению к самому себе.

Далее выясним, ортогональна ли сумма сигналов s0(t) и s1(t) каждому из этих сигналов в отдельности.

Сумма сигналов s0(t)+s1(t), а также произведения сигналов (s0(t)+s1(t))*s0(t) и (s0(t)+s1(t))*s1(t) приведены на рис.11, рис.12 и рис.13.

Рис.11. Осциллограмма суммы сигналов s0(t) и s1(t).

Рис.12. Осциллограмма произведения сигналов s0(t)+s1(t) и s0(t).

Рис.13. Осциллограмма произведения сигналов s0(t)+s1(t) и s1(t).

Покажем, что ни пара сигналов s0(t)+s1(t) и s0(t), ни пара сигналов s0(t)+s1(t) и s1(t) не являются ортогональными.

(s0(t)+s1(t))*s0(t) = s0(t)*s0(t) + s1(t)*s0(t). Как было замечено выше (вывод после рис.4 и вывод после рис.5), пара сигналов s1(t) и s0(t) являются ортогональными, а пара сигналов s0(t) и s0(t) таковой не является. Следовательно, пара исходных сигналов s0(t)+s1(t) и s0(t) не является ортогональной. Аналогичная ситуация и для второго случая.

Для порядка приведем осциллограммы скалярных произведений исходных пар сигналов (рис.14 и рис.15).

Рис.14. Скалярное произведение сигналов s0(t)+s1(t) и s0(t).

.

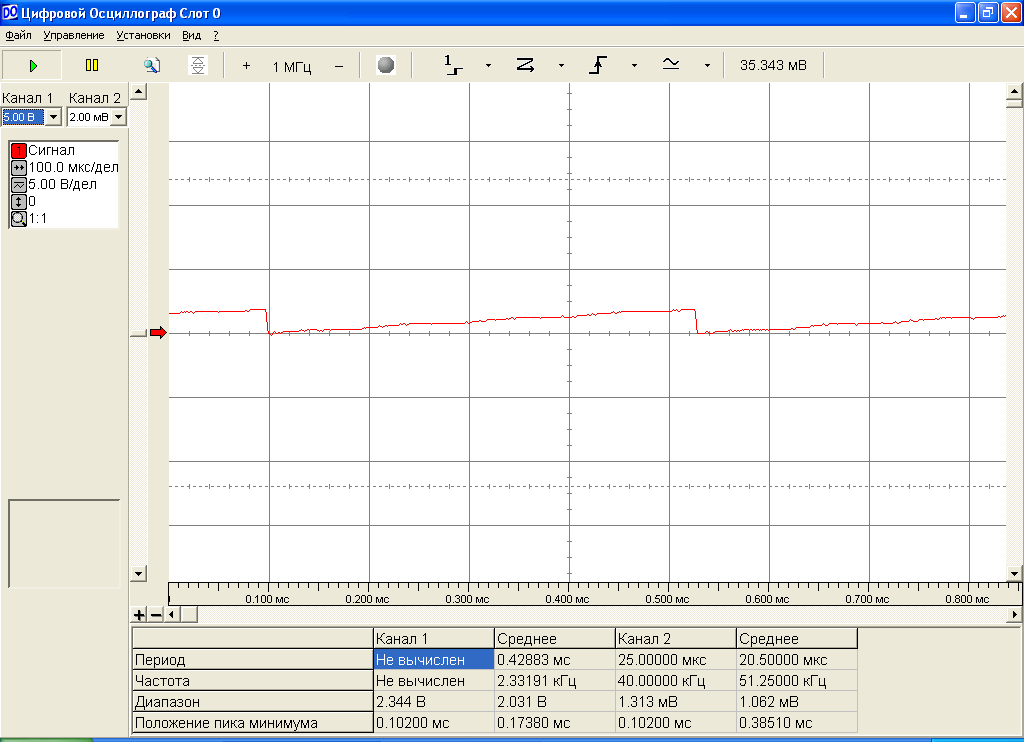
Рис.15. Скалярное произведение сигналов s0(t)+s1(t) и s1(t).

Как видно на рис.14 и рис.15, скалярное произведение за период не равно нулю, и пары исходных сигналов s0(t)+s1(t) и s0(t), а также s0(t)+s1(t) и s1(t) не являются ортогональными.

Теперь попробуем отключить какой-либо из входных сигналов сумматора. Очевидно, что мы на выходе интегратора получим либо тот же сигнал, что и на рис.14 и рис.15 (если на вход интегратора будут подаваться одинаковые сигналы), либо получим почти полное отсутствие сигнала, как на рис.5 и рис.9, что соответствует ортогональности двух сигналов (в этом случае на вход интегратора будут подаваться разные сигналы – этот случай рассматривался на рис.5 и рис.9).

Дата добавления: 2015-10-21