Комплексный спектр сигнала

Разложение периодической функции f(t) с периодом Т показывает, что она имеет частотные составляющие с угловыми частотами w₀, 2w₀, 3w₀, …, nw₀, …. Периодическая функция обладает своим спектром частот. Если известна f(t), то можно определить спектр и наоборот, по спектру найти f(t).

Следовательно, возможно временное и частотное представление функции f(t). При частотном представлении сигнала применяют спектр амплитуд и спектр фаз гармоник. Это дискретные (линейчатые) спектры, которые изображаются графически.

Применение разложения в экспоненциальный ряд является более предпочтительным. Периодическая функция выражается суммой экспоненциальных функций с частотами 0, ±w₀, ±2w₀ и т.д.

Значение отрицательных частот имеет следующее объяснение. Сигналы e^jwt и e^-jwt изменяются с одинаковой частотой w. Их можно представить двумя векторами, вращающимися в противоположных направлениях. Эти вектора при сложении дают действительную функцию времени e^jwt + e^-jwt =2coswt.

Коэффициент F_n является комплексным и характеризуется величиной и фазой, поэтому для частотного представления необходимы два спектра – спектр амплитуд и спектр фаз.

Рассмотрим пример. Пусть f(t)=|Asinpt|. Разложение f(t) в комплексный ряд имеет вид

, w₀ = 2p, Т=1, ,

.

Спектр функции f(t) представлен на рис.3.1.

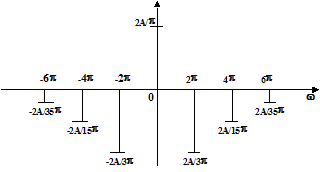
Рис.3.1

Амплитуды всех гармоник – действительные величины, поэтому необходим график одного спектра.

Спектр амплитуд любой периодической функции симметричен относительно оси 0y. Действительно, из формул (1.6) следует, что F_n и F_-n – комплексно сопряженные величины, т.е. F_n=F_-n^*, | F_n |=| F_-n |.

Следовательно, спектр амплитуд представляет собой четную функцию от w. Если F_n - действительная величина, то и F_-n тоже действительная величина и F_n=F_-n. Если F_n – комплексная величина, то , , следовательно, спектр фаз – нечетная функция относительно оси 0y.

Дата добавления: 2015-10-21