Модель Гилберта

Канал может быть в двух состояниях – хорошем и плохом [4]. В хорошем состоянии ошибки быть не может, а в плохом состоянии ошибки возникают с вероятностью e. Последовательность состояний {C_i} образует простую цепь Маркова. Модель Гилберта соответствует схеме М.

Если k=2, e₀=0, e₁=e, то статистика {Е_i} полностью определяется матрицей переходных вероятностей

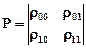
и величиной e.

Чтобы возможно было отобразить группирование ошибок в пакеты, вероятности изменения состояний должны быть значительно меньше вероятностей их сохранения, т.е. r₀₁<<r₀₀, r₁₀<<r₁₁. Вероятность ошибки в канале

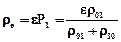
обычно меньше условной вероятности ошибки в пакете e (r_е<<e).

Вероятность возникновения пакета ошибок с данного символа

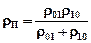(r_П=Р₀r₀₁)

при группировании больше r_е, поэтому r₁₀<e.

При r₁₀=r₁₀, r₀₁=r₁₁ получим канал без памяти.

Последовательность состояний {C_i} по модели Гилберта может также рассматриваться как процесс восстановления с конечным временем, для которого

Р(l)=r₀₁r₀₀^l-1, Р(l)=r₁₀r₁₁^l-1,

или как процесс с мгновенным восстановлением, для которого

Р(l=0)=r₁₁ Р(l)=r₁₀r₀₁r₀₀^l-1,

или как процесс с мгновенным отказом, для которого

Р(l=0)=r₀₀, Р(l)=r₀₁r₁₀r₁₁^l-1, (l>0).

Дата добавления: 2015-10-21