Помехи в каналах связи

Помеха – мешающий передаче сигналов фактор. Совокупность мешающих факторов классифицируют в зависимости от характера воздействия на сигнал, причины и места возникновения, спектрального состава и методики оценки. По характеру воздействия различают аддитивную и мультипликативную помехи.

При аддитивных помехах некоторая электрическая величина u_п(t) суммируется с сигналом u^*(t)=u_с(t)+u_п(t). Степень воздействия определяется соотношением мощностей сигнала и помехи.

Аддитивная помеха обуславливается возникновением в КС случайных ЭДС. Основными причинами аддитивных помех являются различного рода флуктуации, конструктивные недостатки аппаратуры, помехи за счет попутных сигналов и нелинейных переходов.

Мультипликативная помеха рассматривается как электрическая величина, воздействие которой определяется - u^*(t)=u_с(t)´ u_п(t).

Мультипликативные помехи обуславливаются случайными изменениями коэффициентов передачи КС. Основные причины мультипликативных помех:

- неточная компенсация изменений амплитудно-частотной характеристики (АХЧ) линейного тракта системами автоматического регулирования уровня (АРУ) сигнала;

- неисправность в устройствах АРУ;

- ошибочные действия технического персонала;

- нарушения контактов в местах соединений;

- переключения генераторного оборудования;

- переключения дистанционного и станционного питания.

Наиболее распространенной моделью непрерывного КС с аддитивной помехой является гауссовый канал. Помеха в нем аддитивна (h(t)=1) и представляет собой нормальный эргодический процесс с нулевым математическим ожиданием. Одномерная плотность вероятности этого процесса имеет вид

.

Дисперсия s² есть средняя мощность помехи, рассеиваемая на сопротивлении R=1 Ом. Такая помеха называется белым шумом.

Если в канале присутствует только мультипликативная помеха, то он называется каналом с релеевскими замираниями. Плотность величин h(t)ÎH(t) определяется релеевским распределением:

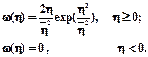
Дата добавления: 2015-10-21