Представление произвольной функции на бесконечном интервале

Непериодический сигнал можно выразить непрерывной суммой (интегралом) экспоненциальных функций.

Существует два способа представления.

1. Функция f(t) выражается через экспоненциальные функции на конечном интервале (-T/2<t<T/2), а затем выполняется условие T®¥.

2. Способ сводится к созданию периодической функции с периодом T, которая совпадает с f(t) только в пределах одного периода. При T®¥ оказывается, что периодическая функция имеет один единственный период на интервале (-¥<t<¥), что соответствует функции f(t).

Первый и второй способы существенно не различаются, но второй более удобен.

Пусть задана функция f(t), гипотетический вид которой показан на рис.3.2. Эту функцию надо представить на интервале (-¥<t<¥) суммой экспоненциальных функций.

Рис.3.2

Построим новую периодическую функцию, в которой f_Т(t) повторяется через Т секунд. Вид функции f_Т(t) показан на рис.3.3.

Рис.1.3

При T®¥ будет выполняться условие 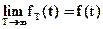. Таким образом, ряд Фурье, представляющий функцию f(t) на бесконечном интервале, будет также представлять f(t) при T=¥.

Для функции f_Т(t) разложение в ряд имеет вид

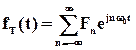, где .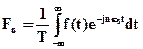

Пусть T®¥, тогда w₀®0 и спектр становится плотнее (чаще). При T®¥ амплитуды F_n®0, но они существуют на любой частоте, т.е спектр из дискретной функции превращается в непрерывную.

Введем новые обозначения nw₀ = w_n. Так как F_n функции от аргумента w_n, то заменим F_n на F_n(w_n). Обозначим TF_n(nw₀) = TF_n(w_n) = F_n(w_n).

Тогда

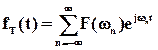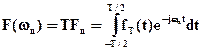, . (1.9)

Так как T=2p/w₀, то

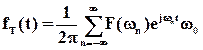. (1.10)

Равенство (1.10) говорит о том, что f_Т(t) можно выразить суммой экспоненциальных функций с частотами w_i, i=1,2,..,n. Амплитуда составляющей на частоте w_n равна F(w_n)w₀/2p, т.е. пропорциональна F(w_n).

Графическая иллюстрация формулы (1.10) представлена на рис.3.4.

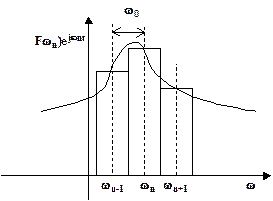
Рис.3.4

Если F(w_n)e^jwnt - действительные величины, то формула (1.10) есть сумма площадей прямоугольников. Чем меньше w₀, тем лучше точность аппроксимации. При T®¥ w₀®0 обозначим через dw. Сумма в уравнении (1.10) переходит в интеграл. Кривая оказывается непрерывной функцией частоты и записывается через F(w)e^jwt. При T®¥ f_Т(t) ® f(t) и формулы (1.9) и (1.10) имеют вид

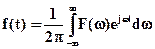, (1.11)

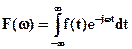. (1.12)

Функция F(w) является частотным спектром функции f(t) и называется функцией спектральной плотности. Уравнение (1.12) – прямое преобразование Фурье, а уравнение (1.11) – обратное преобразование Фурье.

Дата добавления: 2015-10-21