Квантование сигнала

При квантовании сигналов на дискретные значения разбивается Х - область изменения сигнала [11]. На рис.2.11 приведена иллюстрация квантования сигнала x(t).

Интервал квантования Dx=x_i-x_i-1, i=1,2,…,n, n – число квантов. Наименьшее значение сигнала x_min соответствует нижней границе x₀ первого уровня квантования, а наибольшее значение сигнала x_max соответствует верхней границе x_n n -го уровня квантования.

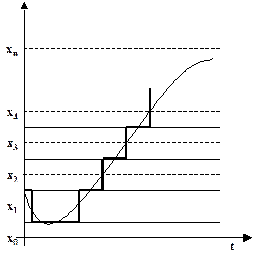
Рис.2.11

Мгновенное значение сигнала x(t)Î(x_i-1,x_i) заменяется величиной 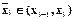, которая называется уровнем квантования.

При равномерном квантовании

.

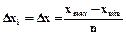При замене истинных значений сигнала уровнями квантования существует ошибка (шум): 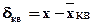, x(t)Î(x_i-1,x_i).

При равномерном квантовании d_КВ минимальная, если уровни выбираются в середине интервала квантования, т.е.

.

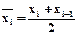Тогда d_КВmax=0,5Dx, диапазон изменения ошибок - 0,5Dx£d_КВ£0,5Dx.

Сигнал x(t) случаен, поэтому ошибка квантования также случайная величина.

Математическое ожидание и дисперсия ошибок зависят от закона распределения сигнала, числа уровней квантования, размера интервала квантования.

Пусть сигнал описывается законом распределения плотности вероятностей w(t). Тогда, если квантуемая величина и процесс квантования независимы,

, .

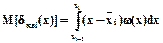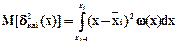Если Dt®0, то 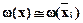, тогда

,

.

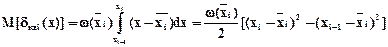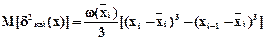Если 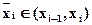находится в середине интервала квантования, то ошибка имеет нормальное распределение, для которого

.

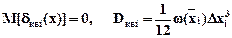Дисперсия d_КВ с учетом изменений сигнала по всем диапазонам значений от x_min до x_max определится по формуле

.

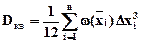При Dx_iºconst, i=1,2,…,n 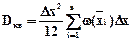, но 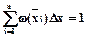, поэтому 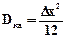. Следовательно, среднеквадратичная ошибка квантования определится по формуле 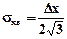, т.е. среднеквадратичная ошибка квантования в Ö3 раз меньше, чем d_КВmax.

Если s_КВ задана, то при равномерном квантовании требуемое число уровней квантования определится по формуле

.

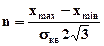Дата добавления: 2015-10-21