Разложение периодической функции в ряд Фурье

Множество, включающее функции cosnw₀t и sinnw₀t (n=0,1,2,…), является полным и ортогональным на интервале (t₀,t₀+2p/w₀). Любую периодическую функцию можно представить в виде разложения на интервале (t₀,t₀+2p/w₀) в виде ряда Фурье [10, 12]

f(t)=a₀+a₁cosw₀t +a₂cos2w₀t +….+a_ncosnw₀t +…

+b₁sinw₀t +b₂sin2w₀t +…b_nsinnw₀t +…. (1.1)

где w₀ - частота первой гармоники, а T=2p/w₀ - длительность интервала разложения (период первой гармоники).

Коэффициенты спектра разложения определяются по формулам (см. формулу (1.4) разд1.2)

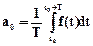, (1.2)

, (1.3)

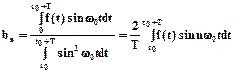, (1.4)

Множество комплексных экспоненциальных функций 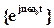(n=0,1,2,…) ортогонально на интервале (t₀,t₀+2p/w₀). Тогда функцию f(t) можно представить на интервале (t₀,t₀+2p/w₀) в виде разложения в экспоненциальный ряд Фурье

. (1.5)

Коэффициенты F₀, F_n и F_-n спектра разложения определяются по формулам

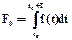; ; . (1.6)

Учитывая, что =cosnw₀t+jsinnw₀t, =cosnw₀t-jsinnw₀t, подставив выражения экспонент, выраженных через тригонометрические функции, в ряд (1.5), получим формулы, устанавливающие связи между коэффициентами a_n, b_n и F_n:

а₀=F₀, a_n=F_n+F_-n, b_n=j(F_n+F_-n), F_n=0,5(a_n-jb_n), F_-n=0,5(a_n+jb_n).

Для формулы (4.1) определим коэффициенты a_k=c_kcosj_k, b_k=c_ksinj_k, тогда, учитывая, что , получим 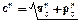, tgj_k=b_k/a_k.

Ряд (1.1) можно записать в вещественной форме (обобщенный ряд Фурье):

, (1.7)

где c_k, j_k, kw₀ - соответственно амплитуда, фаза и частота k–ой гармоники. Угловая частота основной гармоники равна w₀=2p/T.

Рассмотрим пример разложения f(t)=At, (0<t<1) на [0,1], Т=1, w₀=2p/T=2p, t₀=0. Тогда f(t)=a₀+a₁cos2pt +a₂cos4pt +…+b₁sin2pt +b₂sin4pt +…. Коэффициенты разложения определятся по формулам:

, ,

.

Разложение f(t) в ряд Фурье примет вид

.

Разложение этой же функции f(t) в экспоненциальный ряд Фурье будет иметь вид

F₀=А/2, , .

Дата добавления: 2015-10-21