Спектры сигналов, модулированных по частоте

При частотной модуляции амплитуда модулированного напряжения остается постоянной, а частота изменяется в соответствии с законом изменения модулирующего сигнала [14]. Напряжение, модулированное по частоте, изобразим в виде вектора U₀ºconst, который вращается с изменяющейся скоростью w, как это показано на рис.4.11.

Мгновенное значение напряжения U(t) определится по формуле U=U₀cosQ. Так как w=dQ/dt, то .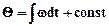

Постоянная интегрирования определяет положение вектора в начальный момент отсчета t=0, т.е. j₀=const. Тогда мгновенное значение напряжения, модулированного по частоте, определится по формуле .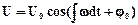

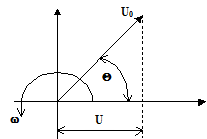
Рис.4.11

Если Dw - наибольшее изменение частоты (девиация частоты), то информационный сигнал - w=w₀ + Dwx(t).

Мгновенное значение напряжения определится

. (2.2)

При фазовой модуляции величины U₀ и w₀ постоянны, а фаза изменяется по закону: Q=w₀t+Djx(t)+ j₀, где Dj - девиация фазы (наибольшее отклонение вектора на временной диаграмме).

Мгновенное значение напряжения, модулированного по фазе, определится по формуле U=U_ФМ=U₀cosQ=U₀cos(w₀t+Djx(t)+ j₀).

Пусть x(t)=cosW₁t и j₀=0. Тогда мгновенное значение напряжения, модулированного по частоте, исходя из формулы (2.2) определим

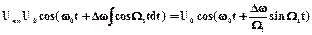. (2.3)

Величина b=Dw/W₁ называется индексом частотной модуляции. Частота модулированного сигнала изменяется по закону:

.

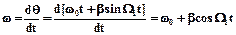Очевидно, что w_max=w₀ + Dw, w_min=w₀ - Dw.

Для разложения сигнала по формуле (2.3) на гармонические составляющие применим разложение cos(x+y)=cos(x)cos(y)-sin(x)sin(y). Тогда

U_ЧМ=U₀cos(w₀t+bsinW₁t)=

=U₀cos(w₀t)cos(bsinW₁t)-U₀sin(w₀t)sin(bsinW₁t); (2.4)

; ,

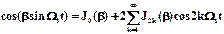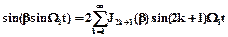где J_2k и J_2k+1 - функции Бесселя четного и нечетного порядков.Учитывая, что sin(x)sin(y)=0,5cos(x-y)–0,5cos(x+y), cos(x)cos(y)=0,5cos(x-y)+0,5cos(x+y), получим окончательное разложение в ряд формулы (2.3)

U_ЧМ=U₀(J₀(b)cosw₀t-J₁(b)cos(w₀-W₁)t+J₁(b)cos(w₀+W₁)t-J₂(b)cos(w₀-2W₁)t+J₂(b)cos(w₀+2W₁)t- J₃(b)cos(w₀-3W₁)t+

+J₃(b)cos(w₀+3W₁)t - …) (2.5)

На рис.4.12 приведен спектр сигнала x(t)=cosW₁t при частотной модуляции.

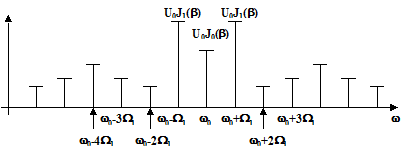
Рис.4.12

Возможная девиация частоты Dw зависит от требований к помехозащищенности передачи и ширины выделенной полосы частот. Чем больше Dw, тем больше уровень восстановления первичного сигнала в приемнике и тем большую полосу должен иметь канал.

Исследуем, как зависит необходимая ширина спектра ЧМ-сигнала от индекса частотной модуляции b.

Пусть b®0, тогда в формуле (2.4) cos(bsinW₁t)»1, sin(bsinW₁t)»bsinW₁t, а

U_ЧМ=U₀cosw₀t-U₀sin(w₀t)(bsinW₁t)=

=U₀cosw₀t-0,5bU₀cos(w₀+W₁)t+0,5bU₀cos(w₀-W₁)t.

Таким образом, при b®0 спектр ЧМ-сигнала, как и спектр АМ-сигнала, состоит из трех гармоник. Следовательно, наименьшая ширина спектра такая же, как и у АМ-сигнала.

С ростом b учитывается все большее число составляющих. Происходит перераспределение энергии по гармоникам, т.к. число их возрастает.

Частотная модуляция с небольшим b называется узкополосной. При данной модуляции выдвигаются повышенные требования к стабильности несущей частоты.

Обычно для практически неискаженной передачи срезают все боковые составляющие, амплитуды которых не превышают 10-12% от амплитуды U₀ несущей частоты.

При b<1 достаточно передать по одной верхней и одной нижней боковой частоте. Ширина спектра при этом не зависит от девиации и равна 2W₁.

При больших индексах модуляции b>1 частотную модуляцию называют широкополосной. Ширина спектра примерно равна 2Dw=(w_max - w_min) и не зависит от частоты модулирующего сигнала W₁.

Дата добавления: 2015-10-21