Графен. Понятие элементарной ячейки. Векторы трансляций.

Графен. Идеальный (бездефектный) графитовый слой является примером двумерной системы с трансляционной симметрией по двум направлениям и характеризуется двумя элементарными векторами трансляций, и :

, где 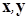- единичные векторы.

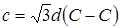Длина вектора , где 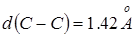- длина связи между атомами углерода, рис. Элементарная ячейка графита содержит два атома углерода.

Векторы с целыми и 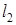образуют прямую решетку графита. Разложение периодической функции в ряд Фурье для двумерного случая имеет вид:

Базисные векторы обратной решетки и определяются с помощью уравнения: , откуда можно получить: , .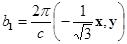

Абсолютная величина этих векторов . Векторы обратной решетки определяют положение всех узлов. Первая зона Бриллюэна имеет вид правильного шестиугольника.

Разложение по векторам обратной решетки имеет вид: и обладает периодичностью прямой решетки .

Оператор Гамильтона инвариантен относительно трансляций и в двумерной системе, поэтому электронная плотность для графитового слоя является периодической функцией вектора трансляций, а его волновая функция должна удовлетворять тереме Блоха. Важная роль теоремы Блоха заключается в том, что оператор Гамильтона не смешивает блоховских функций с разными значениями :

при .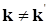

Дата добавления: 2015-09-02