Приближение Хартри-Фока

Прим при моделир стацион-х многоэл-х систем. Соответствующая волновая функция записывается в виде определителя Слэтера: , Физич смысл записи многоэл-й волн фу-и в виде антисиммеризированного произведения одноэлектронных волновых функций состоит в том, что каждому электрону приписывается своя волновая функция 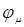, кот назыв спин-орбиталью. Каждая спин-орбиталь явл произв фун , зависящей только пространственных координат электрона, на спиновую фун-ю. называется орбиталью. Для атомов это атомная орбиталь (АО), для молекул – молекулярная орбиталь (МО). В кристаллах или полимерах с трансляционной симметрией функции называют блоховскими функциями.

Представление волновой функции в виде определителя Слэтера обеспечивает условие антисимметричности многоэлектронной волновой функции относительно перестановок электронов. Перестановке электронов соответствует перестановка строк в определителе, при этом определитель умножается на -1.

Множитель необходим для нормировки многоэлектронной волновой функции, при этом орбитали считаются ортонормированными:

Уравнения Хартри-Фока для оптимизированных одноэлектронных функций записываются в следующем виде:

, Доп член, появившийся в уравнениях, описывает обменное взаимодейстсвие, в отличие от прямого взаимодействия в приближении Хартри. Соответствующий вклад в полную энергию называется обменной энергией и равен:

Орбитали многоатомной системы при заданном расположении ядер вместе с соответствующими одноэлектронными уровнями энергии 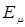рассчитываются в соответствии с вариационным принципом минимизации полной энергии. Явный вид орбиталей находится из одноэлектронного уравнения Шредингера: ,; ; . 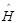оператор Хартри-Фока включает оператор Екин одного электрона, равный и слагаемое, учитывающее Епот . описывает кулоновское взаимодействие: притяжение электрона всеми ядрами системы и отталкивание электрона от всех остальных электронов, а также обменное взаимодействие, зависящее от конкретного вида выбранных волновых функций . Система уравнений Хартри-Фока также, как и уравнения Хартри решается методом итераций. Итеративный процесс продолжается до тех пор, пока энергии и вид орбиталей не перестанут различаться на предыдущем и последующем шаге. Этим методом получены решения для всех основных атомов и ионов, рассчитаны вид атомных орбиталей и их энергии. Недостатком метода является его ограниченная пригодность для расчета многоатомных систем вследствие их низкой симметрии.

Дата добавления: 2015-09-02