Многоэлектронная волновая функция и ее свойства и Определитель Слэтера

Фок заново получил результат Хартри исходя из вариационной процедуры, в котором волновая функция была произведением одноэлектронных волновых функций. Чтобы полная волновая функция меняла знак при обмене местами любой пары электронов, берется линейная комбинация произведения волновых функций. Соответствующая волновая функция записывается в виде определителя Слэтера: 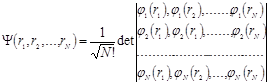, Физич смысл записи многоэл-й волн функц в виде антисиммеризированного производноэлектронных волновых функций состоит в том, что каждому электрону приписывается своя волновая функция 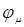, которая называется спин-орбиталью. Каждая спин-орбиталь является произведением функции , зависящей только пространственных координат электрона, на спиновую функцию. Функция 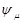называется орбиталью. Для атомов это атомная орбиталь (АО), для молекул – молекулярная орбиталь (МО). В кристаллах или полимерах с трансляционной симметрией функции 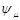называют блоховскими функциями. Представление волновой функции 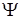в виде определителя Слэтера обеспечивает условие антисимметричности многоэлектронной волновой функции относительно перестановок электронов. Перестановке электронов соответствует перестановка строк в определителе, при этом определитель умножается на -1.

Множитель 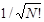необходим для нормировки многоэлектронной волновой функции, при этом орбитали считаются ортонормированными: .

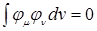Дата добавления: 2015-09-02