Приближение Хартри

Хартри предложил вариационную процедуру, в которой волновая функция аппроксимируется произведением одноэлектронных функций и одновременно минимизируется энергия . При этом не выполняется требование антисимметрии волновой функции и не учтено наличие спина электрона, но достигается достаточно хорошее приближение в определении энергии.

Уравнения Хартли для многоэлектронной системы, позволяющие получить одноэлектронные волновые функции, имеют вид: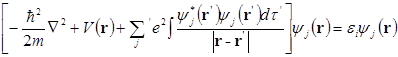

Суммир вып по всем занятым сост, кроме состояния . Уравнения Хартли в этой записи предст собой одноэлектронные уравнения, в которых потенциал, действующий на каждый электрон, определяется значением среднего распред всех других электронов:

Величины в действительности не равняются одноэлектронными энерг. В сист взаимодейств частиц одночастичные энергии определить невозможно, т.к. нельзя произвольно отнимать энергию у одной частицы и отдавать другой, сохраняя лишь полную энергию системы. Далее, полная энергия системы не равна сумме одноэлектронных энергий . Это обнаруживается при анализе выражения, характеризующего полную энергию.

, При суммировании взаимодействие каждой пары электронов учитывается дважды: при вычислении первого электрона и при вычислении той же величины для второго электрона. Поэт, при вычисл эн из суммы необходимо вычесть энергию взаимодействия.

Ур-ия Хартри решаются методом итераций, Для этого задаются некоторой совокупностью приближенных собственных функций, рассчитывают потенциал, и заново определяют собственные функции. Далее процесс повторяется. Процедура является сходящейся и позволяет получить одноэлектронные собственные функции, самосогласованные с потенциалом.

Согласие теории и эксперимента проверяется в одной точке: сравнением полной энергии.

Дата добавления: 2015-09-02