Читайте также:
|
Расчет волновых функций многоатомных систем по уравнениям Хартри-Фока оказывается чрезвычайно трудоемким, вследствие их низкой симметрии. Дальнейшие приближения сводятся к тому, искомые орбитали разлагаются по базису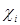 
. Молекулярная орбиталь выражается взвешенной суммой: 
, 
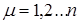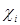, Где - функция, вид которой различается в зависимости от метода, 
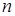- общее число функций, включенных в базис 
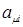- коэффициенты, определяющие вклад базисной функции 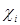в собственную функцию 
. Функции считаются всюду непрерывными и дифференцируемыми.
Т.о., коэффициенты 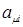фактически и определяют вид обиталей многоатомной системы. При подстановке в одноэлектронное уравнение Шредингера с использованием вариационного принципа Релея-Ритца секулярное уравнение имеет вид: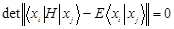 
, В развернутом виде:
, 
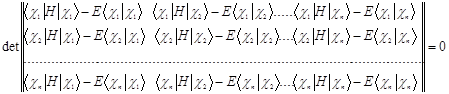
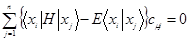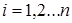, Коэфф 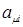и энергии орбиталей находятся из соотношений:
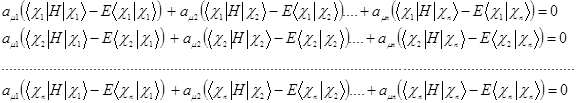
Однозначно 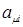определяются из условия нормировки. Здесь 
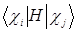- матричные элементы оператора Хартри-Фока; 
- интегралы перекрывания.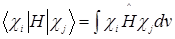 
; 
.
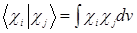Дата добавления: 2015-09-02; просмотров: 300 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Многоэлектронная волновая функция и ее свойства и Определитель Слэтера | | | Орбитали двухатомных молекул |