Трансляционная симметрия полимеров

Полимер, обладающий трансляционной симметрией, рассматривается как одномерный (квазиодномерный) кристалл.

Элемен ячейка предст собой минимальный фрагмент, трансляцией котор воспроизводится вся структура полимера. В качестве простейшей структуры можно представить себе цепочку атомов углерода с с одинаковыми расстояниями между атомами. Совокупность векторов 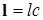, образует прямую одномерную периодическую решетку. Такой структурой обладает углеродный нанопровод, - карбин.

У полимера с трансляционной симметрией в направлении гамильтониан инвариантен относительно трансляций: , Электр плотн полимера также явл функцией вектора трансляций: .

Период-я функция всегда может быть представлена рядом Фурье: = .

Введем одномерную обратную решетку 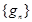, как совокупность точек на оси , отстоящих друг от друга на расстоянии , с координатами:

Разлож в терминах обратного пространства приобретает более компактный вид: и носит название разложения в ряд по обратной решетке. Это разложение обладает трансляционной периодичностью функций:

Коэффициенты разложения равны:

В общем случае волновая функция полимера не является периодической функцией вектора трансляций: . Но вследствие того, что электронная плотность состояний полимера удовлетворяет условию и является периодичной, квадрат волновой функции также является периодической функцией, и, следовательно: Это уравнение называется теоремой Блоха. Величина имеет размерность обратной длины, определена в обратном пространстве с точностью до периода (обратной длины ). Пусть .

Тогда: .

Величина называется волновым вектором (или квазиимпульсом), значения выбирают в интервале , в так называемой первой зоне Бриллюэна.

В расчетах часто принимается, что полимер состоит из конечного числа элементов повторяющихся элементов. Для исключения влияния концевых эффектов считают, первая ячейка соединена с последней. Этот прием называется введением циклических условий Борна-Кармана.

После проведения трансляций циклический полимер переходит сам в себя: .

Из приведенного соотношения следует, что на интервале дискретных значений, отвечающей условию: ,

Если достаточно велико, порядка числа Авогадро, то электронное строение линейной цепочки и замкнутого кольца различаться не будут. Если гамильтониан 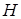характеризуется трансляционной симметрией, а функции и не являются собственными функциями оператора 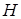, удовлетворяют теореме Блоха, то оператор 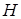не смешивает этих функций: , если . Это следует из:

При

Дата добавления: 2015-09-02