Дроссельдеу процесі

Дроссельдеу деп сұйық (газ) ағыны қысымының қоршаған ортамен жылу алмаспай төмендеуін айиамыз. Іс жүзінде мұндай құбылыс ағынның жолында жергілікті кедергі болған жағдайда кездеседі. Жергілікті кедергінің вентиль, диафрагма, капилляр т.б. болуы мүмкін.

Қимасы тұрақты горизанталь құбырда тоңазытқыш заттың диафрагмада дроссельдеу процесін қарастырып көрелік (4- сурет).

4 - cурет. Жұмысшы денені дроссельдеу схемасы

Тоңазытқыш зат суретте көрсетілген бағытта жылжиды. Құбырдың қимасы Ғ. Ағынның диафрагма алдындағы параметрлері: P₁,υ₁,T₁: диафрагмадан кейінгі параметрлері: P₂,υ₂,T₂. Бірер уақытта I-I қимадағы ағын S₁ жол жүрсе, II-II қимадағы ағын S₂ жол жүріп өтеді. P₁> P₂; υ₂> υ₁ болғандықтан S₂ > S_1.

S₁ жол жүру үшін L₁=P₁.S₁·F жұмыс істеу керек. Осы уақытта диафрагмадан өткен тоңазытқыш зат көлемі V₁=S₁·F немесе V₁₌υ₁·G болады. G-диафрагмадан өткен тоңазытқыш заттың массасы. Олай болса L₁=P₁·υ₁·G.

II-II қимадағы газ мөлшерін жылжыту үшін ағынның жұмсаған жұмыс шамасы: L₂₌P₂·υ₂·G

Берілген уақытта тоңазытқыш заттың берілген массасын жылжыту үшін жұмсалған жұмыс

L=L₂-L₁=(P₂υ₂-P₁υ₁)·G (1.3)

мұндағы: L₁ - I-I қимада ағынды жылжытуға келтірілген жұмыс;

L₂ - II-II қимадан кейінгі газды жылжыту үшін ағынның жасаған жұмысы.

Жалпы бұл жұмыс диафрагма кедергісін басып өту үшін жұмсалады да кедергіден өтерде жылуға айналып, жылу ағынның өзіне беріледі. Дроссельдеу процесі қоршаған ортамен жылу алмаспай өтетін болғандықтан, бұл жұмыс тек жүйенің ішкі энергиясы есебіненн жұмсалуы мүмкін. Демек,

L=(U₁-U₂)·G (1.4)

мұндағы: U₁ және U₂- тоңазытқыш заттың бірлік массасының диафрагмаға дейінгі және диафрагмадан кейінгі ішкі энергиясы.

Осыдан:

(1.5)

немесе

(1.6)

мұндағы: = i₁–ағынның диафрагма алдындағы энтальпиясы;

= i₂ – ағынның диафрагмадан кейінгі энтальпиясы.

Егер i₁=i₂ болса, дроссельдеу процесінде ағынның энтальпиясы өзгермейді. Дәлірек айтсақ, диафрагма қимасы құбыр қимасынан аз болғандықтан ағын диафрагмадан өтерде өзінің жылдамдығын ұлғайтады, оның кинетикалық энергиясы артып, энтальпиясы төмендейді. Диафрагмадан өткен соң, құбыр қимасы үлкен болғандықтан, ағынның жылдамдығы азайып, оның кинетикалық энергиясы төмендейді де энтальпиясы бұрынғы қалпына дейін көтеріледі. Бұл құбылыс 5- суретте келтірілген диаграммадан анық көрінеді. 1-а процесі қысымның Р₁- ден Р₂- ге дейін төмендегендегі энтальпияның азаюы, а-2 процесі диафрагмадан кейін ағынның тежелуі, энтальпияның бастапқы мәнінен дейін көтерілуін көрсетеді.

5-сурет. Дроссельдеу үрдісінің i -S диаграммасы

Дроссельдеу процесінде ағын температурасының өзгеретінін 1854 жылы Джоуль және Томсон байқаған. Сондықтан дроссельдеу процесін Джоуль-Томсон эффектісі деп атайды. Джоуль –Томсон эффектісі дифференциальды және интегралды деп ажыратады.

Дифференциалды эффекті деп–температураның шексіз аз өзгеруінің қысымның шексіз өз өзгеруіне қатынасын айтады. Математикалық символы былай жазылады

(1.7)
Мұндағы i-тек қана дроссельдеу процесіне тән, яғни энтальпияның өзгермейтіндігін көрсетеді. Джоуль-Томсонның дифференциалды эффектісінің аналитикалық формуласын термодинамиканың I және II заңына сүйене отырып анықтауға болады. Осы заңдарға сәйкес энтальпияның өзгеруі:

d_i=dq+υ·dP (1.8)

dg=T·dS

Дросселдеу процесінде i₁=i₂ болғандықтан d_i=0 немесе

0=dq+υ·dP; (1.9)

немесе

T·dS+υ·dP=0 (1.10)

Энтропия зат күйінің функциясы болып табылады:

S=f(T,P) (1.11)

Температура мен қысым арқылы энтропияның толық дифференциалын анықтауға болады:

(1.12)

Осыны ескере отырып (1.12) теңдеуді былайша қайта жазамыз:

(1.13)

Термодинамикадан:

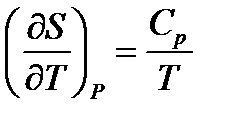; (1.14)

Ендеше (6) теңдеуді қайта жазуға болады:

(1.15)

Бұл теңдеуді енді мына түрге келтіреміз:

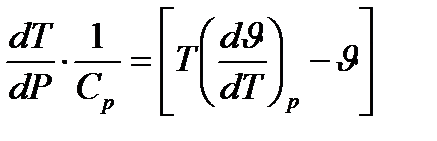(1.16)

(1.7) және (1.16) теңдеулерді салыстыра отырып (1.16) теңдеудің Джоуль-Томсонның дифференциалды эффектісінің аналитикалық формуласы екенін аңғаруға болады.

(1.17)

Енді осы формуланы төменгі температураны алу тұрғысынан талдап көрейік. Дроссельдеу процесіне қысым әрқашан төмендейтін болғандықтан dP<0, ал болады. Олай болса dT температураның өзгеруі α_i таңбасына байланысты.

1. Егер >u_i болса α_i> 0, ал < 0- температура төмендейді.

2. Т _р ˂ болса ˂ 0, ал dT > 0 – температура жоғарылайды.

3. Т _р = болса = 0, ал dT = 0 – температура өзгермейді.

Тоңазытқыш заттың алғашқы күйіне байланысты Джоуль-Томсонның дифференциалды эффектісінің таңбасы әр түрлі болуы мүмкін.

Егер реалды газдар үшін > 0 болса, dT ˂ 0 – дроссельдегенде газдың температурасы төмендейді.

Егер ˂ 0 болса, dT > 0 - дроссельдегенде газдың температурасы жоғарылайды.

Егер = 0 болса, dT = 0 - дроссельдегенде газдың температурасы өзгермейді.

Келтірілген формула бойынша мағанасын білу үшін газ күйінің теңдеуін білу керек.

Дата добавления: 2015-10-23