Математическое моделирование механической части электропривода с учетом упругости

В переходных (динамических) режимах, все элементы механических звеньев, к которым прикладывается момент, подвергаются деформациям. Рассмотрим процесс передачи момента от двигателя до рабочей машины:

Рис.4.3. Соединение двигателя и рабочей машины

Между двигателем (Д) и рабочей машиной (РМ) всегда есть участок вала длиной 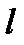(рис.3.18). Представим, что двигатель и рабочая машина соединены резиновым валом. Когда начинает оборачиваться двигатель, то сначала происходит скручивания вала. Конец вала со стороны двигателя оборачивается, а конец вала со стороны рабочей машины еще неподвижен. Происходит деформация вала. Согласно закону Гука, возникающие упругие моменты пропорциональные угловым деформациям:

,

где 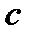- коэффициент упругости.

Расчеты коэффициентов упругости механических соединений при моделировании вызывает самые большие трудности. Расчеты некоторых коэффициентов 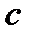можно выполнить последующим выражениям.

Для стальных валов

,

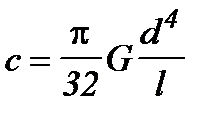где 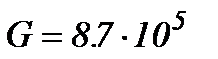кг/см²; Н/ м ²; - диаметр и длина вала, см.

Для стальных канатов (линейная деформация) во время многоразового подъема

,

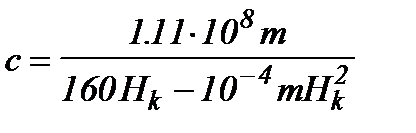где 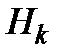- длина каната, м; 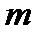- запас упругости каната.

С увеличением значения коэффициента упругости 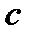механическая часть становится более жесткой и деформация уменьшается.

При 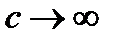движение, переданное от Д к РМ, не перекручивается и механическую часть привода можно рассматривать как одномассовую систему (рис.3.19):

Рис.4.4. Эквивалентная одномассовая система

Момент инерции рабочей машины приводится к валу двигателя. Скорости двигателя и рабочей машины совпадают. В некоторых случаях коэффициент жесткости 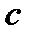окажется небольшим и деформация становится существенной. Например: конвейеры, шахтные подъемные установки (ШПУ). Таких масс, соединенных валами, может быть несколько. Анализ многомассовых систем чрезвычайно сложный, поэтому все маховые массы по обыкновению сводят к двух: двигателя с моментом инерции 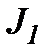и рабочей машины отделенной упругим моментом 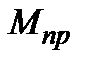и моментом инерции .

Такая механическая структура представляет собой двухмассовую систему (рис.3.20).

Рис.4.5. Эквивалентная двухмассовая система с упругой связью

Угловая деформация упругого элемента может быть выражена:

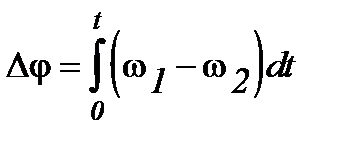. (4.1)

Уравнение движения 1-й массы

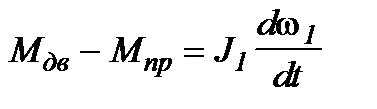. (4.2)

Уравнение движения 2-й массы

. (4.3)

Окончательно система дифференциальных уравнений двухмассовой системы:

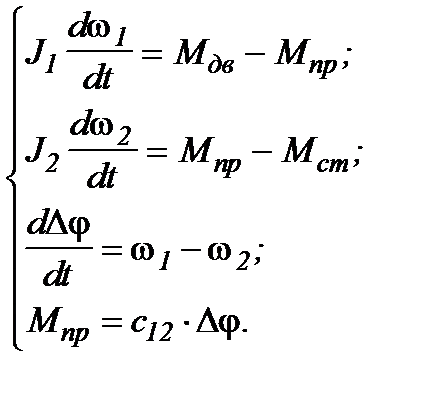(4.4)

Структурная схема двухмасовой системы, составленной по уравнениями (4.4), приведенная на рис.4.6.

Рис.4.6. Структурная схема двухмассовой системы

Таким образом, двухмассовая механическая система представляется структурной схемой с перекрестными обратными связями, то есть имеет повышенную склонность к возникновению колебательных режимов. Данная система получена при условии, что моментом внутреннего трения на валу можно пренебречь, поскольку более существенным оказывается момент внешнего сопротивления, вызванный нагрузками.

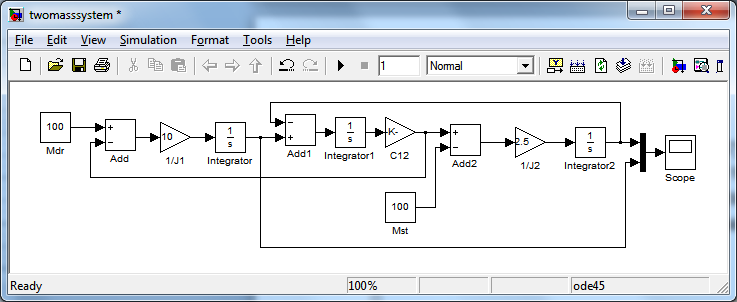
На рис.4.7. приведен вариант реализации механической части двухмассовой системы с упругой связью между отдельными движущимися массами.

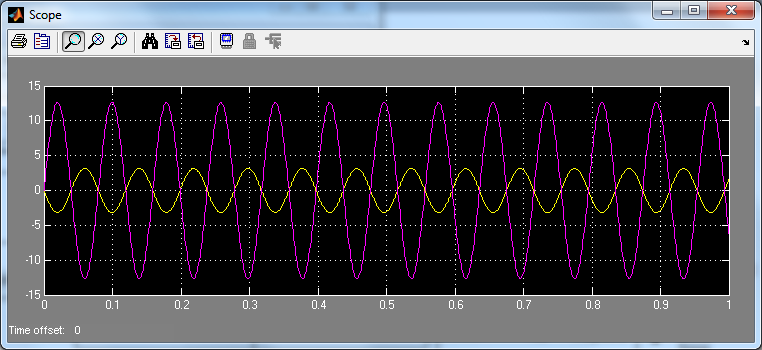
Рис.4.7. Структурная схема (а) и графики угловых скоростей (б) двухмассовой системы в Simulink.

Очень важным при моделировании динамики движения двухмассовой системы является выбор шага интегрирования, поскольку от этого зависит объем исчислений и точность получаемого результата. Ориентиром в этом вопросе могут быть динамические свойства системы, которые определяются резонансными частотами:

.

Для трехмассовой механической системы определяется также частота свободных колебаний при взаимодействия второй и третьей масс:

.

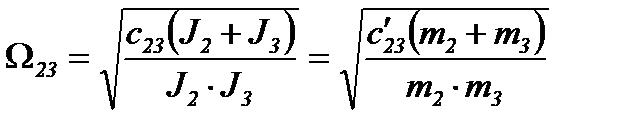Для каждого колебания нужно рассчитать не меньше как 25-30 точек, то есть шаг интегрирования принимается таким:

,

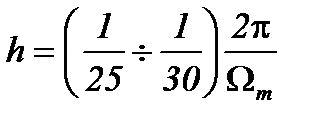где 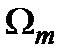- большая из частот.

Дата добавления: 2015-10-29