
Читайте также:
|
Передаточные механизмы, которые соединяют двигатель и рабочую машину не всегда представляют собой сплошные валы, планетарные передачи или канаты. В большинстве случаев между двигателем и рабочей машиной устанавливают редукторы для изменения скорости обращения. Механическое соединение с помощью шестерен нуждается в учете влияния зазора на динамику двухмассовой механической системы. Рассмотрим уравнение двухмассовой системы при этом условия.
Наличие зазора делает зависимость 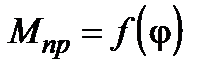 нелинейной. Для учета этой нелинейности рассмотрим влияние зазора на примере зубчатой передачи (рис.4.8.).
нелинейной. Для учета этой нелинейности рассмотрим влияние зазора на примере зубчатой передачи (рис.4.8.).

Рис. 4.8. К определению зазора в механической передаче
В начале движения ротора двигателя рабочая машина остается неподвижной из-за зазора. Упругий момент при этом 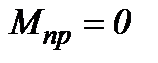 . После выбирания зазора рабочая машина начинает оборачиваться. Появляется упругий момент. На участке выбора зазора зависимость
. После выбирания зазора рабочая машина начинает оборачиваться. Появляется упругий момент. На участке выбора зазора зависимость 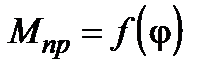 имеет вид нелинейности типа "нечувствительность"
имеет вид нелинейности типа "нечувствительность"
Величина зазора 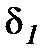 и
и 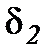 зависит от начального положения передачи. По обыкновению берут
зависит от начального положения передачи. По обыкновению берут
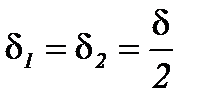 , (4.5)
, (4.5)
где 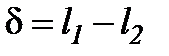 .
.
Система дифференциальных уравнений двухмассовой механической системы с учетом зазора имеет вид (4.6). Структурная схема, которая отвечает данной системе уравнений приведенная на рис.4.9.a.
Пример.
Рассчитаем динамику двухмассовой системы при пуска с постоянным движущим моментом. Исходные дани для расчетов приведенные в таблице 4.1.
Таблица 4.1. Исходные дани для расчетов динамики двухмассовой системы с упругими связями и зазором в передаче.
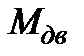 ,Нм ,Нм
| 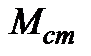 ,Нм ,Нм
| 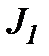 ,кгм2 ,кгм2
|  ,кгм2 ,кгм2
| 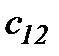
| 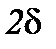 , с-1 , с-1
|
| 100 | 50 | 0.1 | 0.4 | 5000 | 0.1 |
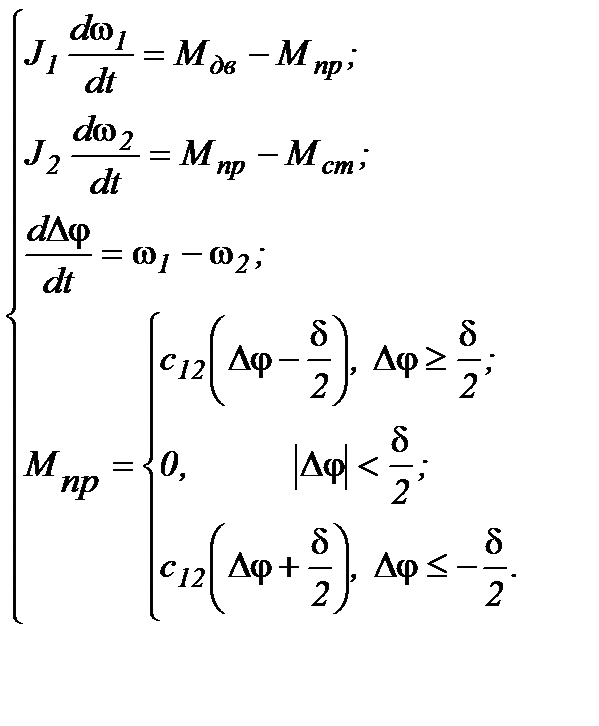 (4.6)
(4.6)
Для моделирования используем модель изображенную на рис.3.24. Шаг интегрирования составляет 0.001 с.
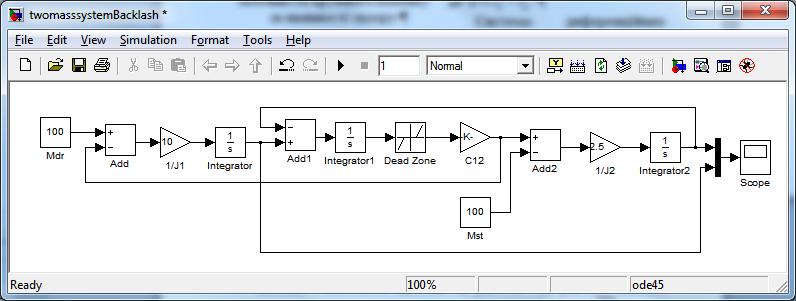
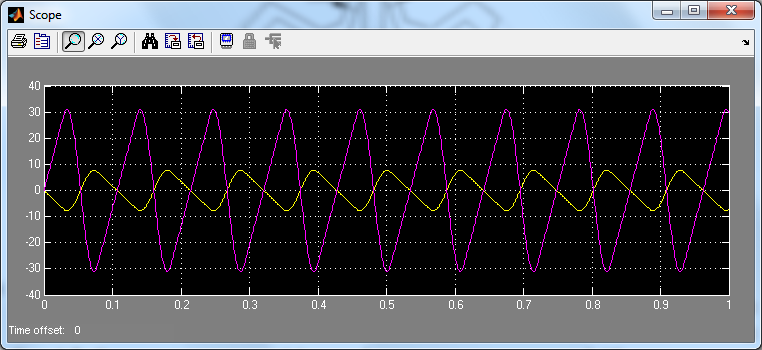
Структурная схема модели при использовании расширения пакета MATLAB - SIMULINK приведенная на рис.4.9, б. На рис.4.9, в приведены графики расчетов колебаний угловых скоростей первой и второй массы

|
|
|
| Рис.4.9. Структурная схема (а) и графики угловых скоростей (б) двухмассовой системы с зазором в механической передаче в Simulink. |
Сравните графики 4.9, в и 4.7. б.
Дата добавления: 2015-10-29; просмотров: 177 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Математическое моделирование механической части электропривода с учетом упругости | | | Момент сопротивления кузнечно-штамповочных машин. |