
Читайте также:
|
Практически все задачи, которые возникают при моделировании электроприводов, сводятся к решению систем нелинейных дифференциальных уравнений. Математический аппарат для аналитического решения таких задач или слишком громоздкий или отсутствующий. За этих условие единым выходом является применения численных методов интегрирования систем дифференциальных уравнений.
Решение систем нелинейных дифференциальных уравнений состоит в нахождении зависимостей 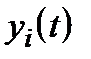 при известных начальных условиях
при известных начальных условиях 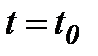 (начальное время) и
(начальное время) и 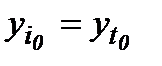 (начальные значения сменных системы).
(начальные значения сменных системы).
Все известные численные методы решения систем дифференциальных уравнений делятся на два класса - одношаговые и многошаговые. Реализация одношаговых методов состоит в разложении искомой функции в ряд Тейлора, в котором содержится то, другое ли число членов, которое определяет порядок метода 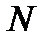 . При одношаговых методах решения каждое новое значение
. При одношаговых методах решения каждое новое значение 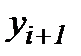 находится за одним известным предыдущим значениям
находится за одним известным предыдущим значениям 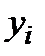 . В качестве примера реализации одношагового метода приведем простейший метод Ейлера первого порядка:
. В качестве примера реализации одношагового метода приведем простейший метод Ейлера первого порядка:
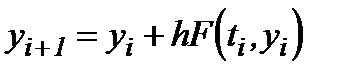 , (2.5)
, (2.5)
где 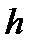 - шаг интегрирования.
- шаг интегрирования.
Суть данного метода состоит в замене интегральной кривой на каждом шагу интегрирования отрезком прямой.
Более сложным, но и более точным есть метод Рунге - Кутта 4-го порядка, который реализуется такими формулами:
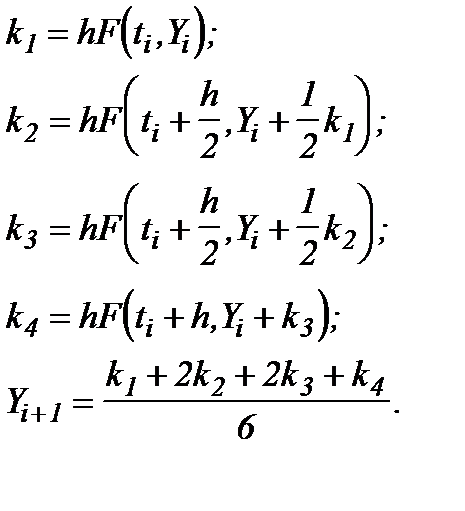 (2.6)
(2.6)
Таким образом, при использовании метода Рунге-Угла 4-го порядка необходимо сделать четыре вычисления правых частей системы дифференциальных уравнений. Поэтому время вычислений для этого метода существенным образом возрастает, но точность существенным образом высшая.
Одношаговым методам присущее свойство "самостоятельного старта", а также есть сравнительно простая возможность изменения шага интегрирования в процессе вычислений.
Реализация многошаговых методов заключается в том, что в них по ряду предыдущих значений 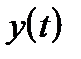 вычисляется последующее значение функции. Порядок метода равняется числу используемых предыдущих значений функции. К данной группе методов принадлежат: группа методов Адамса, метод Милна, метод Хеминга, группа методов прогноза и коррекции.
вычисляется последующее значение функции. Порядок метода равняется числу используемых предыдущих значений функции. К данной группе методов принадлежат: группа методов Адамса, метод Милна, метод Хеминга, группа методов прогноза и коррекции.
Существующие методы численного интегрирования дифференциальных уравнений можно классифицировать как явные и неявные; - одно- и многошаговые (табл.2.1), где 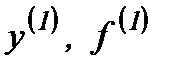 - значение сменной и ее производной после первого цикла расчетов;
- значение сменной и ее производной после первого цикла расчетов; 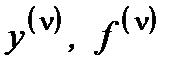 - значение сменной и ее производной после
- значение сменной и ее производной после 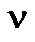 -ї итерации; Я - явный метод; Н - неявный; ОБ! одношаговый; Б - многошаговый; ПК - прогноза и коррекции.
-ї итерации; Я - явный метод; Н - неявный; ОБ! одношаговый; Б - многошаговый; ПК - прогноза и коррекции.
Важным преимуществом многошаговых методов является тот факт, который для вычисления очередного значения интегральной кривой нужное только одно вычисление правых частей системы дифференциальных уравнений, которое заметно ускоряет расчеты. Однако этот метод лишен возможности "самостартования" из-за отсутствия предыдущих значений. Для отыскания этих значений и запуска процедуры многошагового метода необходимо использовать один из имеющихся одношаговых методов.
С помощью явных одношаговых методов значения сменной на 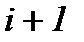 -му шагу интегрирования определяется только на основе информации о значении сменной и ее производной на предыдущем шагу расчетов.
-му шагу интегрирования определяется только на основе информации о значении сменной и ее производной на предыдущем шагу расчетов.
Неявные методы интегрирования используют многократное итерационное уточнение сменной на каждом шагу интегрирования. Итерации выполняют, пока не будет достигнута необходимая погрешность вычислений
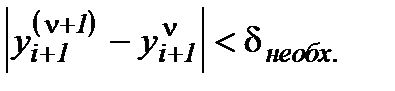 , (2.7)
, (2.7)
или количество итераций не превысит максимальное заданное число 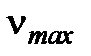 .
.
Погрешность метода численного интегрирования определяется двумя составляющими: погрешностью округления и погрешностью аппроксимации.
Погрешность округления возрастает пропорционально 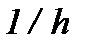 . Для уменьшения этой составляющей погрешности нужно увеличить шаг интегрирования, но при этом начинает возрастать погрешность аппроксимации, которая прямопропорциональна шагу
. Для уменьшения этой составляющей погрешности нужно увеличить шаг интегрирования, но при этом начинает возрастать погрешность аппроксимации, которая прямопропорциональна шагу 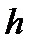 . Через указанные причины возможное неустойчивое решение для устойчивого процесса.
. Через указанные причины возможное неустойчивое решение для устойчивого процесса.
Верхняя граница шага интегрирования может быть определена согласно теореме Котельникова-Шеннона:
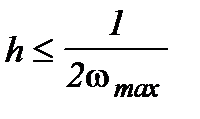 , (2.8)
, (2.8)
где 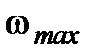 - максимальная частота спектра исследуемого процесса при условии, что значение шага интегрирования удовлетворяет условия стойкости избранного численного метода.
- максимальная частота спектра исследуемого процесса при условии, что значение шага интегрирования удовлетворяет условия стойкости избранного численного метода.
Для получения устойчивого решения при условии, что исследуемая система является устойчивой, а значит все корни 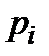 (
(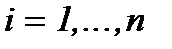 ) характеристического уравнения замкнутой системы находятся в левой плоскости, необходимо и достаточно, чтобы значения были
) характеристического уравнения замкнутой системы находятся в левой плоскости, необходимо и достаточно, чтобы значения были 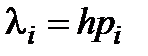 (
(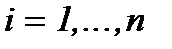 ) расположенные внутри области стойкости данного численного метода. Однако расположение всех
) расположенные внутри области стойкости данного численного метода. Однако расположение всех 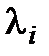 в пределах области устойчивости не гарантирует иногда получения удовлетворительного результата, а действительная область устойчивости оказывается значительно меньшей.
в пределах области устойчивости не гарантирует иногда получения удовлетворительного результата, а действительная область устойчивости оказывается значительно меньшей.
Таким образом, одновременно с общепризнанными точными методами численного интегрирования высокого порядка, например Рунге-Кутта четвертого порядка, Кутта -Мерсона четвертого порядка, на основе которых разработанные стандартные программы численного интегрирования уравнений с постоянным и сменным шагом интегрирования, целесообразно использовать при разработке нестандартных методик моделирования менее точные методы, например Эйлера второго порядка и Адамса-Башфорта, используя которые можно обеспечить достаточную точность моделирования при соответствующем выборе шага интегрирования. При решении задач управления в реальном времени целесообразно использовать экономический как за объемом использованной памяти, так и по времени решения метод Эйлера первого порядка. Особую актуальность это имеет при применении в микропроцессорных системах управления электроприводами. Однако для большинства задач, модели которых построены из элементарных динамических звеньев, выбор шага интегрирования может быть осуществлен по таблице 2.1.
Таблица 2.1.
До вибору кроку інтегрування
| Тип ланки | Передаточна функція | Значення 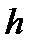
|
| Інтегруюча | 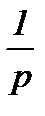
| - |
| Диференціююча | 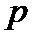
| - |
| Інтегро-диференціююча | 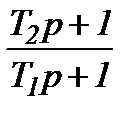
|
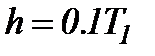
|
| Аперіодична 1-го порядку | 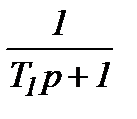
|
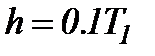
|
| Аперіодична 2-го порядку | 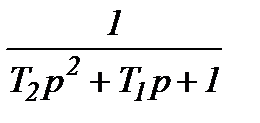
| 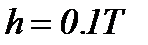 , де , де 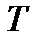 менша з менша з 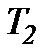 і і 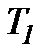
|
| Коливальна | 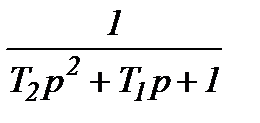
| Менше з 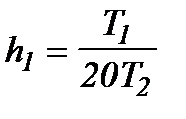 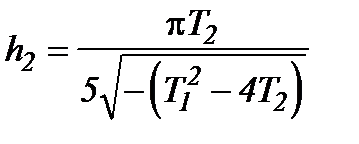
|
Дата добавления: 2015-10-29; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Математическое представление элементов ЭМС | | | Типовой алгоритм и структура программы для решения систем дифференциальных уравнений |