Центральна система

На рис. 11.2 представлена мережа, яка отримала назву центральна система.

Рис. 11.2 – Центральна система

Виміряні 15 кутів. Шуканих пунктів 4. Кількість умовних рівнянь

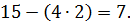
Як це випливає з креслення (рис. 11.2), маємо 5 умовних рівнянь фігур

На пункті В виміряні пункти замикають горизонт, тобто їх сума теоретично дорівнює 360°. Звідси виникає ще одна геометрична умова – умова горизонту.

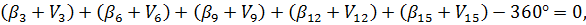
Якій відповідає умовне рівняння

де .

На підставі теореми синусів може бути записана умова полюса вигляду (11.45)

(11.48)

де

Подальша послідовність зрівнювальних обчислень принципово не відрізняється від розглянутої в п. 11.6.1.

Вставлення в жорсткий кут

Як видно з рис. 11.3, в цій системі виміряні 9 кутів. Шуканих пунктів 2.

Кількість умовних рівнянь

Маємо три умови фігур

В цій мережі кутів АОВ – жорсткий кут, бо він дорівнює різниці вихідних дирекційних кутів

де – дирекційні кути ліній OA і OB.

Рис. 11.3 – Вставлення в жорсткий кут

Звідси виникає умова дирекцій них кутів

якій відповідає умовне рівняння

де

В цій мережі сторони ОА і ОВ – жорсткі. Як це видно з рис. 11.3, на підставі теореми синусів можна записати рівняння сторін

Продиференціювавши це рівняння за змінними запишемо умовне рівняння

де

Послідовність подальшої обробки викладена в п. 11.6.1.

Ланцюг трикутників між двома сторонами, довжини

І дирекційні кути яких відомі

В мережі виміряні 15 кутів (рис. 11.4). Так як мережа вільна, кількість шуканих пунктів р = 6, приймаючи до уваги, що координати одного з пунктів або відомі, або приймаються умовно. Відповідно кількість незалежних умов буде дорівнювати

Рис. 11.4 – Мережа трикутників

В цій мережі маємо:

1. П’ять умовних рівнянь фігур

2. Умова дирекційних кутів

якій відповідає умовне рівняння

де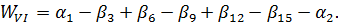

3. На підставі теореми синусів можемо записати умову сторін

Продиференцюємо цей вираз за змінними , і отримаємо умовне рівняння

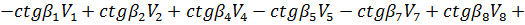
де

Послідовність подальшої обробки викладена в п. 11.6.1.

Дата добавления: 2015-10-29