Лабораторна робота № 2. Цифрове моделювання процесів у системах керування

Цифрове моделювання процесів у системах керування

Мета роботи: вивчення різних способів побудови процесів у лінійних безперервних системах за допомогою ЦОМ; порівняльний аналіз методів дискретизації безперервних передатних функцій.

Зміст роботи

Моделювання безперервних об'єктів і систем керування на ЦОМ (цифровій обчислювальній машині) вимагає опису її динаміки за допомогою дискретної передатної функції. Прикладом дискретного елемента є ЦОМ, що реалізує ПІ-закон керування. Рівняння руху має вигляд:

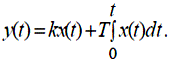
(2.1)

Складемо кінцево-різницеве рівняння по рівнянню руху:

(2.2)

Алгоритм функціонування дискретного елемента описується кінцево-різницевим рівнянням.

Існують чотири форми запису кінцево-різницевих рівнянь:

1. щодо ґратчастих функцій, зсунутих вліво

(2.3)

2. щодо упереджуючих різниць:

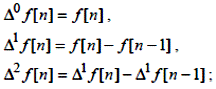
3. щодо ґратчастих функцій, зсунутих вліво

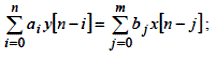
(2.5)

4. щодо відстаючих різниць

(2.6)

визначається також як і Δ

Запишемо кінцево-різницеве рівняння в першому вигляді, тобто:

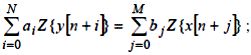
Другий доданок залежить від початкових умов. У випадку якщо до моменту n =0 усі значення x[n] і y[n]=0, тобто задані початкові умови ліворуч, той другий доданок буде звертатися в 0. Тоді передатна функція дискретного елемента має вигляд:

(2.7)

Дискретною передатною функцією системи називається відношення Z перетвореного вихідного сигналу до Z перетвореному вхідному сигналу при нульових початкових умовах.

Дискретна передатна функція безперервного елемента, що функціонує в дискретному режимі рисунок 6.

Рис.6 Функціональна схема безперервного елемента, що функціонує в дискретному режимі

У результаті виходить наведена передатна функція W_П (s), звідки w_п (t) – наведена імпульсна перехідна характеристика.

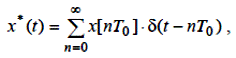
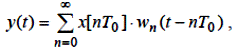
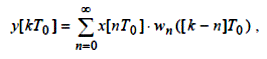
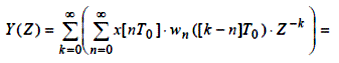
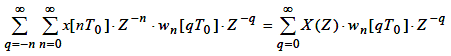
У такий спосіб дискретна передатна функція безперервного елемента обчислюється, як Z-перетворення імпульсної перехідної характеристики, наведеної безперервної частини системи.

Передатна функція цифрової системи керування і умови її фізичної реалізованості. Для виявлення умови фізичної реалізованості запишемо дискретну передатну функцію у вигляді:

Якщо перевести цей запис у кінцево-різницеву форму, то отримаємо наступне вираження:

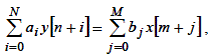
Умова фізичної реалізованості означає, що М < N, а якщо ні, то вихідного сигналу буде залежати від майбутнього значення вхідного сигналу, що суперечить принципу причинності (казуальності).

Імпульсна система стійка тоді і тільки тоді, коли її реакція на будь-який обмежений вплив обмежене.

Одержимо умову стійкості в тимчасовій області.

Введемо обмеження на вхідний вплив.

|g [ k - n ]| ≤ M, при будь-яких значеннях аргументу. Де М –

деяке велике число. Далі одержимо:

Вище наведена нерівність випливає з визначення стійкості в тимчасовій області, отже для стійкості дискретних систем необхідно, щоб:

що є умовою стійкості в тимчасовій області. В такому випадку імпульсна система стійка, якщо ряд дискрет її імпульсної характеристики абсолютно сходиться. Іншим словами абсолютна збіжність ряду дискретної імпульсної характеристики є необхідною й достатньою умовою стійкості.

Одержимо умову стійкості в частотній області.

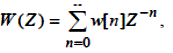
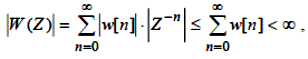
З умови |Z|<1. Остання нерівність означає, що передатна функція повинна бути обмежена за межами одиничної окружності комплексної площини Z.

Іншими словами W (Z) не повинна мати полюсів за межами одиничної окружності.

Для дослідження стійкості імпульсних систем у частотній області використовується аналог критерію Михайлова. Даний критерій випливає з ознаки аргументу. Формулювання полягає в наступному: різниця між кількістю нулів і полюсів функції f (z), замкнених усередині замкненої кривої, дорівнює зміні аргументу функції f (z) при обході крапкою Z контуру в позитивному напрямку, ділене на 2π.

Z = e-jφ = e ^Jω, де ω – відносна частота.

Якщо φ = [0,2 π], те ϖ = [-π, π], звідси маємо:

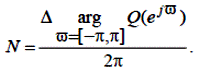
де N – кількість полюсів.

Q (ejϖ) – комплексно-сполучений поліном, звідки можна звузити інтервал відносної частоти ϖ = [0, π], тоді:

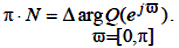
Таким чином формулювання аналога критерію Михайлова полягає в наступному. Для стійкості імпульсних систем необхідно і достатньо, щоб годограф Q (e ^jϖ), при зміні ϖ = [0, π], послідовно проходив проти годинникової стрілки N – квадрантів координатної площини, де N – порядок характеристичного рівняння.

Тому що моделювання безперервних об'єктів і систем керування на ЦОМ вимагає опису її динаміки за допомогою дискретної передатної функції. Подібний аналіз звичайно складається із двох етапів [2]:

– опису безперервної системи за допомогою дискретної моделі;

– особисто цифрового моделювання – побудова на ЦОМ тимчасових процесів при різних вхідних впливах і параметрах системи.

Існують різні методи дискретизації безперервних передатних функцій [3]:

– метод введення фіктивного квантувач фіксатора;

– метод апроксимації операції інтегрування;

– метод апроксимації операцій кратного інтегрування.

Опишемо коротко перших два.

1. На вході аналогової моделі безперервної системи W (s) вводять імпульсний елемент, що включає ідеальний імпульсний квантувач (ідеальний ключ) і формувач імпульсів (фіксатор) W_ф (s) рисунок 7. Таким чином одержують імпульсну модель.

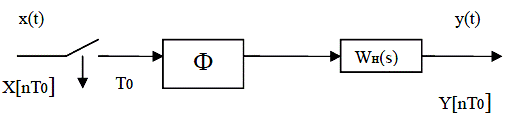
Рис.7. Введення квантувачів у безперервну систему

Для цієї імпульсної моделі відомими методами обчислюють дискретну передатну функцію W (z). Можливе використання різних формувачів імпульсів. Найчастіше це фіксатори імпульсів нульового або першого порядку відповідно

	(2.8)
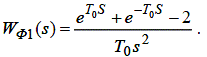
	(2.9)

Тут T ₀ – період квантування.

2. Суть методу полягає в заміні передатної функції інтегратора передатною функцією дигратора, яка формується на основі того або іншого методу інтегрування. Попередньо передатна функція безперервної системи записується щодо змінної s ^-1. Після перетворень одержують дискретну передатну функцію W (z).

Розглянемо види диграторів:

1. Інтегрування по методу правих прямокутників.

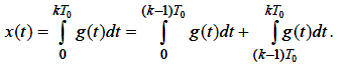
Інтеграл складається з інтегралів на попередніх кроках і на одному останньому кроці.

, тоді звичайно розносне рівняння

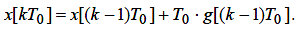
З кінцево-різницевого рівняння одержимо передатну функцію інтегратора:

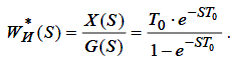
Замінимо кінцево-різницеву форму безперервної:

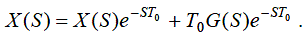
Тоді передатна функція дигратора по методу правих прямокутників має такий вигляд:

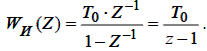
(2.10)

2. Інтегрування по методу лівих прямокутників.

, тоді звичайно розносне рівняння

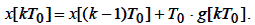
Замінимо кінцево-різницеву форму безперервної:

З кінцево-різницевого рівняння одержимо передатну функцію інтегратора:

Тоді передатна функція дигратора по методу лівих прямокутників має такий вигляд:

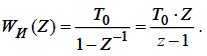
(2.10)

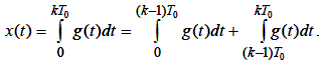
тоді звичайно – розносне рівняння

Замінимо кінцево-різницеву форму безперервної:

З кінцево-різницевого рівняння одержимо передатну функцію інтегратора

Тоді передатна функція дигратора по методу трапецій має такий вигляд:

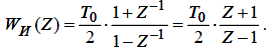
(2.12)

Найбільше часто використовувані передатні функції диграторів наведені в табл. 2.

Побудова тимчасових процесів на ЦОМ по передатній функції дискретної системи W (z) не викликає ніяких труднощів, тому що різницевих рівняння отримані з W (z) являють собою програми рекурентного обчислювального процесу.

Таблиця 2.1

Передатні функції диграторів

Метод інтегрування	ПФ інтегратора	ПФ дигратора
Лівих прямокутників
Правих прямокутників
Трапецій

При переході до власне цифрового моделювання (другий етап) необхідно розв'язати два взаємозалежні питання. По-перше, це вибір періоду квантування T ₀. Значення T ₀ суттєво впливає на точність і час, необхідне для цифрового моделювання. По-друге – питання стійкості. Добре відомо, що якщо безперервна система стійка, те її дискретна модель необов'язково буде стійкою. Властивість стійкості дискретної моделі також буде залежати від величини періоду квантування T ₀.

Дата добавления: 2015-10-24