Порядок виконання роботи. 1. Сформуйте матрицю регресорів і вектор вимірів для наведеного вище прикладу

1. Сформуйте матрицю регресорів і вектор вимірів для наведеного вище прикладу. Перевірте ранг F.

2. Обчисліть вектор МНК-оцінок b і суму квадратів похибки Q.

3. Варіюючи окремо кожний коефіцієнт β _i відносно b_i, побудуйте залежності Q від βi. Зробіть висновки про властивості коефіцієнтів bi.

4. Виконайте пп. 1-3 для завдання побудови лінійної статичної моделі за результатами експерименту, представленим у табл. 4.2.

5. Варіанти набору параметрів вибрати відповідно списку журналу академгрупи.

Таблиця 4.2.1

Результати проведених експериментів

№ п/п	Час, сек.	Живлення, (сек.) т/год.	Витрата газу м^3/год.	Тиск газу на пальнику, атм.	Т, ºС у зоні підігріву
1.		15,6	11,8	0,55
2.		15,4	11,8	0,55
		15,4	11,8	0,55
4.		15,5	11,8	0,55
5.		15,4	11,8	0,55
6.		15,4	11,8	0,55
7.		15,5	11,8	0,55
8.		15,7	11,8	0,55
9.		15,8	11,8	0,55
10.		15,5	11,8	0,55
11.		15,6	11,8	0,55
12.		15,7	12.2	0,55
13.		15.8	12.2	0,55
14.		15,4	11,8	0,55

Продовження таблиці 4.2.1

15.		15.7	11,8	0,55
16.		15.5	11,8	0,55
17.		15.7	11,8	0,55
18.		15.7	11,8	0,55
19.		16.0	12.2	0,6
20.		15.6	12.2	0,6

Таблиця 4.2.2

№ п/п	Т, ºСу зоні кальценув.	Т, ºС відхід газів	Т,ºС вторинний повітря	Т,ºС до ел. ф.	Т,ºС після ел. ф.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.

Таблиця 4.2.3

№ п/п	Разрідж. острац. повітря	Разрідж. колоснику мм. рт. ст.	Разрідж. у курній камері	Навант. в голівці печі 60	Навантаження димососа
1.				2,5
2.				5,0
3.				5,0

Продовження таблиці 4.2.3

4.				5,0
5.				5,0
6.				4,0
7.				4,0
8.				4,0
9.				6,0
10.				7,0
11.				3,0
12.				3,0
13.				2,0
14.				4,5
15.				4,5
16.				4,5
17.				4,0
18.				4,0
19.				3,0
20.				3,0

Таблиця 4.2.4

№ п/п	Навантаження димососа	Тиск під вентилятори, димосос	Тиск під вентилятори, димосос 60	Тиск під вентилятори гол. привід	Гарячою камерою
1.				20,8
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.				20,8
12.
13.				21,4
14.				21,4
15.				21,4
16.				21,8
17.
18.

Продовження таблиці 4.2.4

19.				21,5
20.				21,5

Таблиця 4.2.5

№ п/п	Остр.	Остр	Загальне	Загальне	Аспірація
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.

№ п/п	Аспірація	Дим	Дим	Xз	Xз
1.				7,7	8,9
2.				7,86	8,1
3.				7,7	8,1
4.				7,7	8,7
5.				7,7	8,7
6.				7,8	8,8
7.				7,8	8,8
8.				7,7	8,8
9.				7,6	8,8
10.				6,1	7,5

Продовження таблиці 4.2.5

11.				5,9	7,5
12.				7,8	8,7
13.				5,9	8,6
14.				5,9	8,6
15.				6,0	7,9
16.				6,0	8,5
17.				6,0	8,6
18.				6,0	7,7
19.				5,9	7,3
20.				6,0	7,4

Зміст звіту

Звіт повинен містити: вектор МНК-оцінок; значення мінімальної суми квадратів похибок; результати обчислювального експерименту по п.3; висновки.

Контрольні питання

1. Що називається ідентифікацією статичних характеристик об'єктів керування?

2. Поясніть методику застосування МНК для побудови статичних характеристик об'єктів керування.

3. Виведіть формулу обчислення МНК-оцінок коефіцієнтів керування регресії.

4. Сформулюйте основні гіпотези класичного регресійного аналізу й властивостей МНК-оцінок.

5. Доведіть властивість незміщеності МНК-оцінок.

Лабораторна робота № 5

Ідентифікація динамічних моделей об'єктів і систем

Керування

Мета роботи: вивчення особливостей застосування регресійного аналізу для ідентифікації передатних функцій безперервних об'єктів і систем керування по тимчасових характеристиках.

Зміст роботи

Однієї з основних динамічних моделей лінійних об'єктів і систем керування є передатна функція. При ідентифікації передатної функції необхідно визначити порядок поліномів чисельника і знаменника та їх коефіцієнти за результатами експериментальних досліджень різних частотних або часових характеристик. Надалі будемо починати, що порядок поліномів передатної функції заданий, а експериментальні дані являють собою вхідний і вихідний сигнали системи в часі.

Таким чином, завдання ідентифікації полягає от у чому.

Задана передатна функція у вигляді:

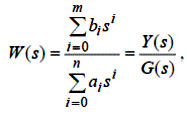
де n і m – відомі натуральні числа, n ≥ m; Y (s) і G (s) – зображення по Лапласу вхідного та вихідного сигналів; a_i і b_i – невідомі коефіцієнти, причому a_n =1.

Нехай експериментальним шляхом отримані дискретні вибірки вхідного g [ kТ ₀] і вихідного y [ kТ ₀] сигналів, де T ₀ – відомий період квантування. Які значення коефіцієнтів a_i і b_i, що щонайкраще задовольняють експериментальним даним?

Якщо в якості критерію ідентифікації, тобто заходи, що відбиває ступінь відповідності моделі та експериментальних даних, обраний мінімум суми квадратів похибки, то рішення завдання ідентифікації одержують за допомогою МНК.

Розглянемо метод найменших квадратів. Оскільки результати спостережень суть випадкові величини, одержати «дійсні» значення коефіцієнтів β _i i =1,2,3,.., k з моделі неможливо:

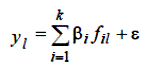
(5.1)

Замість цього можна отримати їхні оцінки b_i i =1,2,3,.., k на основі досліджень по таблиці попередньо складених спостережень. Якщо мова йде про модель (5.1), то вона приймає вигляд:

(5.2)

де y_l – передвіщене значення відгуку і служить оцінкою істинного значення y_l. Величина відгуку служить оцінкою «дійсного» значення η _l. У регресійному аналізі для отримання оцінок коефіцієнтів моделі (5.1) використовується метод найменших квадратів.

Через дію випадкових збурень передбачене значення y_i буде відрізнятися від результату виміру y_l. Різниці:

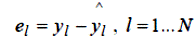
називають залишками.

Тому, що дійсне значення вектора коефіцієнтів β і його оцінка b різні, 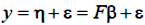, а .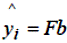

Звідси вектор залишків:

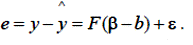
Оцінки коефіцієнтів регресії природно шукати так, щоб забезпечити найменші можливі залишки, але залишки численні, тому потрібна деяка сумарна характеристика, яка повинна залежати від відмінностей між обмірюваними й передвіщеними значеннями вихідних характеристик у кожному досліді. Таку функцію звичайно називають функцією втрат, або функцією ризику. Для різних цілей і умов дослідження вона може мати різний вигляд.

Ось одна з найбільше часто використовуваних функцій втрат:

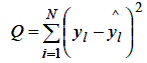
(5.3)

У ній залишки зведені у квадрат, щоб компенсувати відмінності в їхніх знаках.

Запишемо суму (5.3) у векторній формі.

Нехай позначає N -мірний вектор стовпець обмірюваних значень відгуку, а 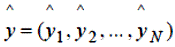– N -мірний вектор відповідних їм передбачених значень, нарешті, 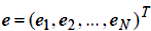– вектор стовпець залишків. Як відомо, скалярний добуток вектора на самого себе дорівнює сумі квадратів його елементів, тому вираз (5.3) можна переписати у вигляді:

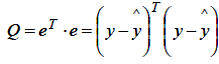
Метод, що дозволяє оцінювати регресійні коефіцієнти, вибирають так, щоб мінімізувати величину Q. Його називають звичайно методом найменших квадратів. Нехай на основі даних таблиці дослідження потрібно знайти такі оцінки коефіцієнтів регресії, які мінімізують суму Q, визначену в (5.3). у силу припущення гіпотези 6 на можливі значення оцінок не накладені ніякі обмеження, тому мінімум, дорівнявши похідні за невідомими оцінками b_i i =1,2,3,.., k. Але спочатку підставимо (5.2) в (5.3):

Після диференціювання цього виразу за шуканими оцінками і дорівнюючи нулю перших похідних, отримаємо систему рівнянь:

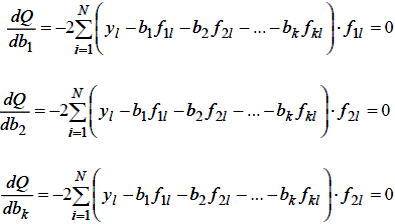
(5.5)

Константи -2, що входять в усі рівняння, не відіграють ролі, тому що для рівності нулю добутку досить, щоб рівними нулю виявилися відповідні суми. Тому отримана система зводиться до вигляду:

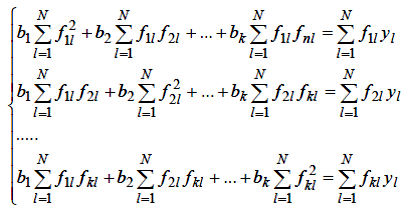
Отримана система є лінійною щодо шуканих оцінок b_i i = 1,2,3,.., k, а число рівнянь у ній дорівнює числу невідомих коефіцієнтів k даноїмоделі. Дана система називається системою нормальних рівнянь.

Запис системи нормальних рівнянь можна спростити, якщо припустити, що:

Очевидно q_ij = q_ji, оскільки порядок перемножування функцій під знаком суми не важливий. У нових позначеннях система нормальних рівнянь прийме вигляд:

Надалі ми скористаємося матричним записом. Позначимо (k × k)– матрицю величин g_ij літерою G, (k ×1) – вектор оцінок шуканих коефіцієнтів літерою b, (k ×1) – вектор правої части системи літерою Z. Тоді:

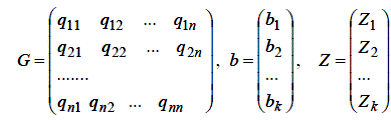
Важливо помітити, що G – симетрична матриця, тому що g_ij = g_ji.

Такий вигляд матиме матричний запис системи нормальних рівнянь:

Матриця G називається інформаційною матрицею. Її можна представити через введену в матрицю 1.2 матрицю регресорів F: G = F^TF. Це твердження перевіряється безпосередньо транспонуванням F і перемножуванням F^T і F. Точно так само перевіряється, що Z = F^Ty. Виходить, систему нормальних рівнянь можна переписати таким чином:

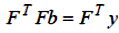
(5.6)

Найчастіше зустрічається матрична форма запису нашої системи.

Якщо виконане припущення 7 (гіпотеза), тобто ранг F рівний k, те ранг F^TF теж рівний k, так як з теорії матриць [12] відомо, що добуток матриць F^T і F є позитивно визначена матриця.

При цих умовах можна отримати матрицю, зворотну до інформаційної. Позначимо її С = (F^TF)^-1 = G^-1. Оскільки (F^T F)^-1 F^TF = 1, множення виразу (5.6) ліворуч на матрицю (F^TF)^-1 приводить до рішення системи нормальних рівнянь:

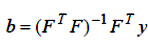
(5.7)

Матриця C =(F^TF)^-1 називається матрицею дисперсій коваріацій, або матрицею похибок. Іноді її називають просто дисперсійною або коваріаційною матрицею.

При неоднорідності і кореляції спостережень. Розглянемо модель динаміки об'єкта, використовувана для опису лінійного стаціонарного процесу (рис.16). Така модель звичайно задається рівнянням розподіленого лагу:

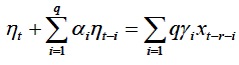
(5.8)

відповідно до якого вихідний сигнал η _t у момент часу t залежить від вихідних сигналів на q кроків назад і від вхідного сигналу x на i-r кроків назад у часі, де r характеризує чисте запізнювання об'єкта. Сигнал η _t зашумлений адаптивним сигналом η _t, з нульовим математичним очікуванням і незалежними значеннями, так що спостережуваний вихідний сигнал:

(5.9)

процесу (5.8) – (5.9) відповідають два наступні рівноцінні записи:

Та

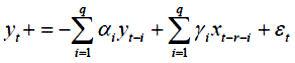
(5.10)

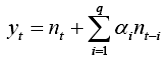
(5.11)

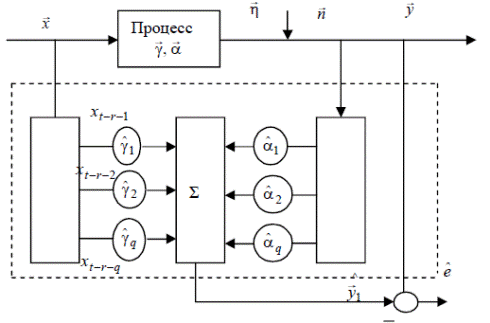
Рис.16. Функціональна схема лінійного стаціонарного процесу

Рівняння (5.10) називається узагальненою регресійною моделлю, а еквівалентне збурення визначається вище описаною сумою, у яку входять елементи шуму. Цю модель можна представити у матричному вигляді:

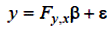
(5.12)

де 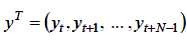– (N×1) – мірний вектор спостереженьвихідного сигналу;

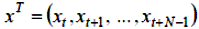– (N×1) – мірний векторвхідного сигналу;

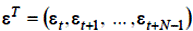– (N×1) – мірний вектор еквівалентної збурюючої дії;

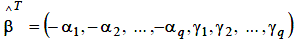– (k×1) – мірний вектор оцінюваних параметрів;

– (N ×1) – мірнийвектор шуму;

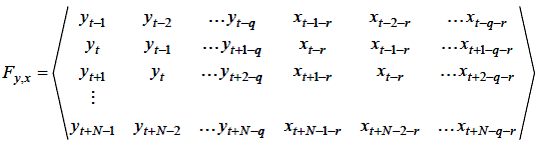
Рівняння (5.12) аналогічно відомій регресійній моделі статики, у якій кожний рядок матриці плану міститься в цьому випадку не різні функції незалежних змінних, а значення вихідного та вхідного сигналів у різні моменти часу. Однак для узагальненої моделі характерна кореляція компонентів еквівалентного впливу, що обурює, ε один з одним і діагональність і матриці V (ε) навіть при некореляційних елементах вектора шуму n. Якщо використовувати (5.12) і врахувати, що E (ε) = 0 при E (n) = 0, то отримаємо наступну формулу для коваріації між двома елементами ε, що знаходяться на s інтервалів у часі, наприклад ε_tі ε_{t+ s}:

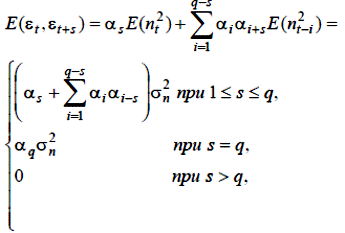
(5.13)     (5.14)   (5.15)

де σ₂ ⁿ – означає дисперсію елементів n. Що стосуються діагональних елементів V (ε), вони всі однакові:

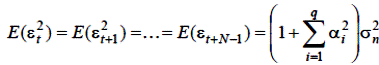
(5.16)

Методика застосування МНК включає 4 етапи.

1. Дискретизація вихідної передатної функції. Дискретизація може бути виконана різними методами, наприклад, методом правих (лівих) прямокутників, методом трапецій і т.д. У результаті формується дискретна передатна функція, що апроксимує вихідну безперервну:

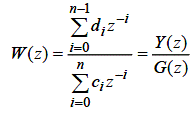
де Y (z) і G (z) – відповідно z-перетворення вихідного та вхідного сигналів;

с_i і d_i – коефіцієнти дискретної моделі, що залежать від коефіцієнтів a_i і b_i вихідної безперервної моделі (з ₀ =1).

Дата добавления: 2015-10-24