Моделювання систем з розподіленими параметрами

Мета роботи: вивчення методики моделювання об'єктів і систем керування, які описуються диференціальними рівняннями в частинних похідних.

Зміст роботи

Завдання моделювання систем з розподіленими параметрами має місце в тих випадках, коли адекватний математичний опис досліджуваних процесів може бути презентовано у вигляді системи диференціальних рівнянь у частинних похідних, граничних і початкових умов. Розробка моделі системи з розподіленими параметрами включає наступні основні етапи:

1. Визначення складу змін, що представляють собою, як правило, функції просторових координат і часу, достатнього для опису динаміки системи.

2. Опис процесів взаємодії між змінними з використанням базових законів і емпіричних співвідношень.

3. Складання системи рівнянь енергетичного й матеріального балансу системи, запис граничних і початкових умов.

Розглянемо поетапно описану методику розробки моделі на прикладі завдання моделювання несиметричного конвективно-кондуктивного нагрівання плоскої тонкої пластини товщиною d у газовому середовищі (рис.17).

Етап 1. Для опису динаміки системи в цьому випадку необхідні наступні змінні: температура газового середовища у верхній поверхні пластини T_гв (x, y, t); температура газового середовища в нижній поверхні пластини T_гн (x, y, t); температура усередині пластини T (x, y, z, t). Далі робиться припущення про незмінність температур по координатах x та y, тобто T_гв (x, y, t) = T_гв (t); T_гн (x, y, t) = T_гн (t); T (x, y, z, t) = T (z, t).

Рис.17 Досліджувана пластина

Етап 2. Передача тепла поверхням пластини від газового середовища проводиться шляхом конвективного теплообміну. Потужність, передана через одиничну площу поверхні тіла, визначається різницею температур газового середовища і поверхні тіла, а також коефіцієнтом тепловіддачі, що залежать від умов конвекції в поверхні:

де h_в і h_н – коефіцієнти тепловіддачі верхньої та нижньої поверхні відповідно. Перенос теплоти усередині пластини здійснюється за рахунок кондуктивного теплообміну відповідно до закону Фур'є:

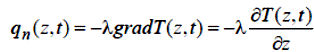
де q_п (z, t) – потужність, передана через одиничну площу; λ – теплопровідність матеріалу пластини.

Тепловою взаємодією бічних поверхонь пластини з газовим середовищем зневажаємо через малу товщину пластини d.

Етап 3. Відповідно до закону збереження енергії, при відсутності всередині тіла джерел тепла, потужність, що поглинається в елементарному об’єму тіла, дорівнює потужності, яка затрачається на зміну температури цього об’єму:

де с – теплоємність матеріалу пластини; ρ – щільність матеріалу пластини. На поверхнях пластини повинен виконуватися баланс теплових потоків конвективної та кондуктивної складових теплообміну:

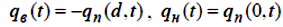
У результаті запишемо систему рівнянь, що описують динаміку несиметричного конвективно-кондуктивного нагрівання плоскої тонкої пластини з врахуванням зроблених припущень:

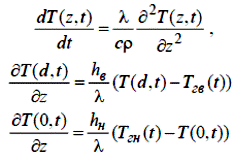
Перший із записаних виразів називають рівнянням теплопровідності, два останні являють собою граничні умови третього роду. Звичайно гранична умова третього роду характеризує закон конвективного теплообміну між поверхнею тіла і навколишнім середовищем при постійному потоці тепла (стаціонарне температурне поле). У цьому випадку кількість тепла, переданого в одиницю часу з одиниці площі поверхні тепла в навколишнє середовище з температурою Т _С в процесі охолодження (Т _П> Т _С), прямо пропорційно різниці температур між поверхнею тіла та навколишнім середовищем, тобто:

де α – коефіцієнт пропорційності, який ще називається коефіцієнтом теплообміну; Т_С – температура середовища; Т_П – температура поверхні.

Отримана система рівнянь дозволяє знайти розподіл температури по товщині пластини T (z, t) для будь-якого моменту часу при заданих законах зміни температури газового середовища у поверхонь пластини T_гв (t), T_гн (t), і відомому початковому розподілі температури T (z,0). Знаходження рішення диференціального рівняння можна здійснити класичними методами: методом поділу змінних і методом джерел, сутність якого полягає в тому, що будь-який процес поширення тепла у тілі теплопровідністю можна представити, як сукупність процесів вирівнювання температури від безлічі елементарних джерел тепла, розподілених як у просторі, так і в часі. Рішення завдання теплопровідності по цьому методу в основному зводиться до правильного вибору джерел і розподілу.

Для багатьох завдань теплопровідності використання класичних методів виявляється неефективним, наприклад, застосування методу поділу змінних для завдань із внутрішніми джерелами тепла. У результаті застосовуються більш зручні операційні методу рішення і кінцеві інтегральні перетворення, що ставляться до методів інтегрального перетворення для рішення диференціальних рівнянь.

Розглянемо методи чисельних рішень завдань теплопровідності. При розгляді систем диференціальних рівнянь із досить загальними крайовими умовами точні методи рішення натрапляють на більші труднощі, які стають непереборними при рішенні нелінійних завдань. У цих випадках доводиться звертатися до тем або іншим чисельним методам рішення. Одним з найбільш застосовуваних є метод кінцевих різниць або метод сіток.

Метод кінцевих різниць заснований на заміні похідних їхнім наближеним значенням, вираженим через різниці значень функції в окремих дискретних крапках – вузлах сітки. Диференціальне рівняння в результаті таких перетворень заміняється еквівалентним співвідношенням у кінцевих різницях, рішення якого зводиться до виконання нескладних алгебраїчних операцій. Остаточний результат рішення дається виразом, по якому значення майбутнього потенціалу (температури) у даній крапці (вузлі) є функцією часу, її «дійсного моменту часу» потенціалу і «дійсного моменту часу» потенціалу суміжних вузлових крапок. Повторюваність операцій при розрахунку полів температури створює більші зручності для застосування обчислювальної техніки, завдяки цьому ефективність роботи в багато разів збільшується.

Наближену заміну першої і другої похідних можна провести наступним чином.

Нехай дана функція y = f (x), графік якої представлено на рисунку 18. Якщо через α_iпозначити кут, утворений з позитивним напрямком осі абсцис дотичній до кривої, проведеної в крапці M (x_i, y_i), те похідна функції при x = x_i визначається за формулою:

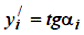
(6.1)

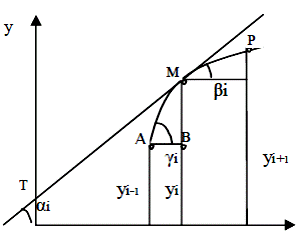
Рис.18. Графік до визначення похідної функції f(x)

Виберемо на кривій дві сусідні крапки A (x_i-1, y_i-1) і P (x_i-1, y_i-1) так, щоб різниці x – x_i-1 = x_{i +1} – x_i = h були б досить малі і приблизно замінимо α _i на β _i або γ _i (або, що те ж саме, розглянемо замість дотичної МТ одну із січних МР або АМ). Тоді:

(6.2)

або

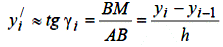
(6.3)

Якщо ж кутовий коефіцієнт дотичної МТ приблизно замінити кутовим коефіцієнтом січної АР, то отримаємо:

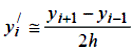
(6.4)

Праві частини формул (6.2) – (6.4) називаються відповідно: різницевим відношенням вперед, різницевим відношенням назад і симетричним різницевим відношенням.

Наближене значення другої похідної y_i′′ функції y = f (x) при x = x_i може бути отримане елементарно, якщо замінити криву на ділянці АР ламаною лінією АМР, що має в крапці М два нахили, тобто:

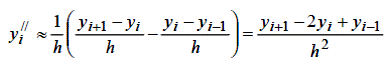
(6.5)

Зрозуміло, що наведені формули (6.2) – (6.5) для заміни похідних різницевими співвідношеннями доцільно проводити інші заміни, однак при чисельному інтегруванні рівнянь теплопровідності найбільше часто застосовують саме ці формули.

Розглянемо, наприклад, одномірне рівняння теплопровідності для ізольованого тонкого стрижня довжиною L:

(6.6)

Тому що функція T (x, τ) залежить від змінних x і τ, тому використовуємо сітку прямокутного типу (рис.19). На осі абсцис відкладаємо відрізок довжиною L і ділимо його на n рівних частин. Отриманий крок на осі абсцис позначимо через h = L / n. Крапки розподілу (вузли) на осі x мають абсциси x = 0, x = h,.., x = L.

По осі ординат відкладемо значення часу τ через рівні проміжки l. Проводимо через отримані вузли на осях координат (на рис.19 вони відзначені хрестиками) прямі, паралельні координатним осям, які утворюють прямокутну сітку. Значення Т у вузлах, що лежать на осях координат і на прямій, паралельній осі ординат і розташованої від неї на відстані L, знаходяться із початкового і граничних умов.

Рис.19. Схема розрахунку по сітці прямокутного типу

Завдання наближеного чисельного інтегрування рівняння (6.6) по методу сіток полягає в знаходженні наближеного значення функції Т у кожному вузлі сітки.

Позначимо через T_i, _k дійсне значення температури в точці стрижня x = i · h в момент τ = k · l, тобто у вузлі, поміченим на рисунку 19, символом k, i.

Замінимо часткові похідні в крапці (ih, kl) через різницеві співвідношення за формулами (6.2) – (6.5).

	(6.7)
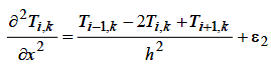
	(6.8)

де ε₁ і ε₂ – залишкові члени, що прагнуть до нуля при прагненні до нуля l і h. Тоді у вузлі (ih, kl) диференціальне рівняння (6.6) заміняється наступним співвідношенням:

	(6.9)
або
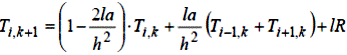
	(6.10)

де R = aε ₂ – ε₁.

Відкидаючи в (6.10) залишковий член, одержуємо різницеве рівняння:

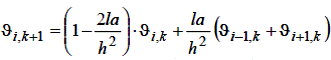
(6.11)

у якому через ϐi_{, k} позначене наближене значення величини T_{i , k} у тому ж вузлі (ih, kl).

Формула (6.11) дозволяє обчислити значення ϐ у вузлах горизонтального ряду (k +1) за значеннями ϐ, що знаходяться тільки в одному попередньому ряді (k). Тому за допомогою формули (6.11) можна знайти значення ϐ у вузлах першого горизонтального ряду (при τ = l) по відомих із крайових умов значеннях температури у вузлах самої осі Оx (при τ= 0). Одержавши таким способом значення ϐ у першому ряді, по тій же формулі знаходимо значення у вузлах другого горизонтального ряду (тобто при τ= 2_l). Цей процес побудови можна продовжувати як завгодно довго, тому що значення температури у вузлах прямих x=0 та x=L будуть відомі із граничних умов. Формулу (6.11) можна вивести, застосовуючи закони Фур'є та Ньютона до складання теплових балансів елементів, на які розбито тіло. Цей спосіб висновку розрахункових формул широко практикується багатьма закордонними дослідниками. Перепишемо, слідуючи Д.Ю. Панову, формулу (6.11) у більш зручному вигляді (див. схему на рис. 20):

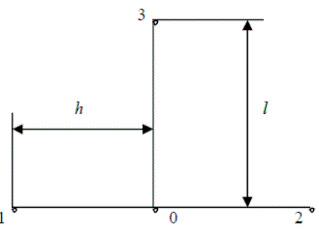
Рис.20 До висновку формули (6.12)

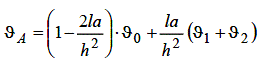
(6.12)

Вибираючи співвідношення між кроками l і h різним чином, з (6.12) можна одержати ряд частих співвідношень.

Так, наприклад, при l = h ²/3 a:

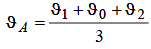
(6.13)

при l = h ²/6 a

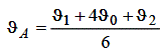
(6.14)

при l = h ²/12 a

(6.15)

і взагалі при l = h ²/ p∙a

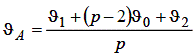
(6.16)

Особливо простий вигляд формула (6.12) одержує при p = 2:

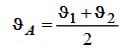
(6.17)

Ця остання формула, названа формулою Є. Шмідта, була вперше отримана Д. Ю. Пановим в 1938 році і має велику практичну перевагу в порівнянні з формулою (6.14) і особливо (6.15), тому що при тому ж h величина l сама більша, а отже, і обсяг обчислювальної роботи при застосуванні (6.17) скорочується в 3 рази в порівнянні з (6.14) і в 6 раз у порівнянні з (6.15). Слід зазначити, через свою простоту формула (6.17) широко використовується при графічному рішенні нестаціонарних завдань переносу.

Дослідження показують, що при р= 1 одержуємо вже розбіжну обчислювальну схему. Взагалі слід зазначити, що при рішенні нестаціонарних рівнянь у частинних похідних параболічного типу питання співвідношення між h і l, а також похибка округлення в чисельному рішенні відіграють першорядну роль, тому що ними визначають збіжність і стійкість отриманих рішень. Зі строгих теоретичних міркувань випливає:

1. користуватися формулою (6.16) можна тільки при р ≥ 2;

2. найбільший крок l дає формула (6.17), тобто при р = 2;

3. формула (6.16) тем точніше, чим більше р.

Розглянута сітка для чисельного інтегрування рівняння (6.6) зручна, коли завдання вирішується при граничних умовах першого роду: у цьому випадку граничні прямі x = 0, x = L належать самій сітці.

Якщо рівняння вирішується при граничних умови третього роду, практика обчислень і теоретичні дослідження показують, що вводити додаткові вузлові крапки, що лежать поза досліджуваною областю. Наприклад, вирішуючи рівняння (6.6) при граничних умовах

(6.18)

сітку потрібно будувати так, щоб права гранична пряма лежала б посередині між двома прямими x = x_n і x= x_{n +1}, а ліва – посередині між прямими x = x ₀ і x = x ₁ (рис. 21) (x = h /2), тобто в розгляди вводяться значення ϐ_{n+1, k} і ϐ_{0, k} – значення функції для крапок, що лежать поза досліджуваною областю.

Похідну 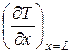, що входить у другу умову (6.18), тобто в крапці B (L, kl), заміняємо симетричним різницевим співвідношенням:

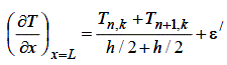
(6.19)

а значення температури на самій поверхні, тобто T (L, kl), беремо як середнє арифметичне значення температур у крапках А и С:

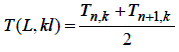
(6.20)

Рис.21. Розрахункова схема для завдання нестаціонарної теплопровідності (граничні умови третього роду)

Тоді умова (6.18) запишеться таким чином:

(6.21)

або переходячи до наближених значень ϐ, одержимо після перетворень такий вираз:

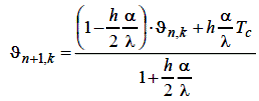
(6.22)

по цій формулі і знаходяться наближені значення функції у вузлах допоміжної прямій x = L + h /2.

Значення ж температури на самій граничній прямій x = L визначається за формулою:

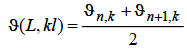
(6.23)

що після перетворень дає:

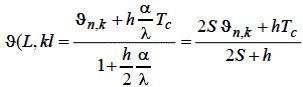
(6.24)

де

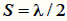
(6.25)

Значення температури у вузлах допоміжної прямої x= - h /2 знаходиться за формулою:

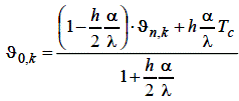
(6.26)

На лівій поверхні отримаємо:

(6.27)

Методика рішення диференціального рівняння теплопровідності із джерелами не відрізняється від вище викладеної. Метод кінцевих різниць дозволяє успішно вирішувати як одномірні, так і дво- і тривимірні завдання. Цей метод має назву явного, оскільки виражає значення ϐ у момент τ _k-1 через момент часу τ_k.

Дата добавления: 2015-10-24