Моделювання систем багатокритеріального керування

Мета роботи: знайомство з інженерною практикою проектування оптимальних систем керування; вивчення типових завдань моделювання оптимальних систем керування.

Зміст роботи

З теорії автоматичного керування нелінійними автоматичними системами керування називаються системи, у структурі яких знаходиться хоча б один нелінійний елемент. Здійснюючий нелінійне перетворення вхідного сигналу.

Розглянемо найпоширеніші статичні характеристики нелінійних елементів, що відбивають явища, що часто зустрічаються в технічних системах, обмеження, нечутливості, тертя, люфти, гістерезис, наявність упорів, стрибкоподібної зміни величин і т.п. При певних допущеннях ці статичні характеристики можуть бути досить добре представлені однозначними або багатозначними кусочно-лінійними непарними симетричними кривими називаними типовими статичними характеристиками.

а) б)

Рис.8. Нелінійні характеристики типу

а) – «зона нечутливості», б) – «насичення»

Проаналізуємо основні типові нелінійності. Нелінійність типу «зона нечутливості». Статична характеристика елемента з нелінійністю такого типу наведено на рисунку 8,а.

«Зона нечутливості», або «мертва зона», виникає в механізмах із пружинним навантаженням, що використовується для зменшення люфту, а також у багатьох інших обладнаннях, не чутливих до малих вхідних сигналів, наприклад, у різного типу вимірювально-перетворювальних елементах (індуктивні, ємнісні, потенціометричні вимірювачі-перетворювачі, тахогенератори), підсилювально-перетворювальних (електронні, магнітні, гідравлічні підсилювачі) і виконавчих елементах. Характеристику нелінійності типу зона нечутливості можна описати наступною залежністю:

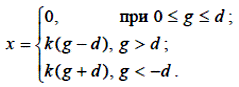
(3.1)

Де величина d визначає ширину зони нечутливості елемента до зміни вхідного сигналу. Нелінійність типу «насичення». Насичення, або обмеження, є, мабуть, найпоширенішим видом нелінійності.

Форма характеристики насичення рисунок 8,б ідентична для багатьох реальних обладнань, хоча вхідні і вихідні величини можуть мати всіляку фізичну природу. Так, практично всі реальні підсилювачі, незалежно від того, чи є вони електронними, магнітними, пневматичними або гідравлічними, мають межу посилення по потужності в області більших вхідних сигналів уже тільки тому, що джерело живлення, за рахунок якого здійснюється посилення вхідного сигналу, обмежений по потужності. Виконавчим елементам також найчастіше властиві нелінійності типу насичення, наприклад, двофазний виконавчий двигун має обмеження по швидкості.

Аналітичне вираження для статичної характеристики типу насичення має вигляд:

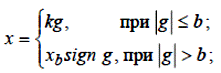
(3.2)

Величина b визначає значення вхідного сигналу, при якому наступає насичення в елементі: х _b – максимально можливий рівень вихідного сигналу.

Нелінійність типу «насичення із зоною нечутливості». Ті самі елементи систем можуть мати як властивість нечутливості, так і властивістю насичення. При малих вхідних сигналах ці елементи поводяться подібно елементу з нелінійністю типу зони нечутливості, а при більших сигналах подібно елементу з обмеженням вихідного сигналу.

Статична характеристика (рис.9) такого типу нелінійності описується так:

(3.2)

Ця типова нелінійність являє собою досить загальний випадок однозначної безперервної нелінійності.

Рис.9. Нелінійна характеристика типу «насичення із зоною нечутливості»

Релейні або інші комутаційні елементи, гідравлічні та пневматичні клапани, фрикційні муфти вносять у роботу системи характер переривчастості. Найпростішою типовою нелінійністю, що має однозначну розривну характеристику, має трипозиційне реле без гістерезису (рис.10). Ця нелінійність характеризується наявністю зони нечутливості шириною 2 b (в інтервалі якої вихідна величина дорівнює нулю) і високого та низького рівнів вихідного Сигналу, що мають місце при всіх значеннях вхідного сигналу, що перевищують по модулю величину b.

Рис. 10. Нелінійна характеристика типу «трипозиційне реле без гістерезису»

В такому випадку характеристика типу трипозиційне реле без гістерезису виражена за допомогою знакової функції:

(3.4)

Нелінійність типу «трипозиційне реле з гістерезисом». Розглянута однозначна релейна характеристика відповідає деякій ідеалізації релейного елемента. У реальних релейних елементах звичайно не збігаються значення вхідного сигналу, при яких відбувається стрибкоподібна зміна вихідного сигналу з нульового рівня на в або нижчий рівні і, навпаки, з високого або низького рівня на нульовий. У результаті з'являється неоднозначність характеристики в деякому інтервалі зміни вхідної величини (рис.11,а), що відповідає типовій нелінійності трипозиційне реле з гістерезисом.

а) б)

Рис. 11. Характеристики типу: а – «трипозиційне реле з гістерезисом»,

б – «двопозиційне реле з гістерезисом»

Математично вона виражається залежністю

(3.5)

Тут m – коефіцієнт, що ухвалює значення з інтервалу (-1,1). Похідна pg = dg / dt вказує на напрямок зміни вхідної координати g, що дозволяє встановити величину вихідного сигналу з врахуванням попередніх значень в інтервалах [ mb, b ], [– mb,– b ], де характеристика двозначна.

Легко помітити, що при m = 1 розглянута характеристика набуває вигляду, що відповідає трипозиційному реле без гістерезису (див. рис.11), а у випадку, коли m = –1, отримаємо характеристику нелінійності типу двопозиційне реле з гістерезисом (рис.11,6).

(3.6)

Таким чином, типова нелінійність (3.6) являє собою найбільш загальний вигляд нелінійностей розривного характеру. Для дослідження нелінійних систем застосовується метод фазової площини. Метод фазової площини належить до точних методів дослідження нелінійних систем, що вимагають рішення нелінійних диференціальних рівнянь руху системи й відображення цього руху на фазовій площині у вигляді деякої кривої, називаною фазовою траєкторією даної системи. Фазова площина являє собою виражений n-мірний фазовий простір, коли число фазових змінних n =2. У загальному випадку при розгляді перехідних процесів нелінійної стаціонарної системи, викликаних якими-небудь початковими відхиленнями координат при відсутності зовнішнього збурювання,тобто для системи, що описуються рівняннями у формі Коші, фазовий простір задається системою координат, по осям якої відкладаються фазові змінні, або змінні стани (х ₁, х_n) системи керування. Тоді початковий стан системи зобразиться певною крапкою Мо з координатами x ₁(t ₀), x ₂ (t ₀),.., x_n (t ₀) n-мірного фазового простору, а перехідний процес, тобто рішення рівняння X (t)={ x ₁(t), x ₂(t),.., x_n (t)} буде являти собою деяку фазову траєкторію (рис.12). Поточна крапка М(1) фазової траєкторії відбиває стан системи керування в довільний момент часу 1 і називається зображаючою крапкою.

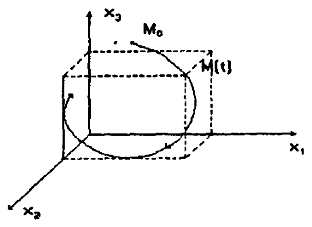
Рис. 12 Фазова траєкторія системи третього порядку в тривимірному фазовому просторі

Безліч фазових траєкторій на фазовій площині, відповідних до безлічі початкових умов, називається фазовим портретом.

Для нелінійних систем з безперервним видом нелінійної характеристики фазові траєкторії, побудовані для різних початкових умов, ніколи не перетинаються.

Якщо система описується, нелінійним диференціальним рівнянням другого порядку:

(3.7)

де F – нелінійна функція, для одержання рівняння фазової траєкторії насамперед необхідно перейти до опису у формі Коші.

Отримаємо:

(3.8)

Щоб виключити час, поділимо друге рівняння системи (3.8) на її перше рівняння:

(3.9)

Рішення отриманого диференціального рівняння і буде являти собою вираження для фазової траєкторії x ₂= f (x ₁). У системі координат (x ₁, x ₂) задаючи фазову площину, по координатних осях координат відкладаються фазові змінні: по осі абсцис – вихідна (керована) координата системи x1, по осі ординат – швидкість зміни керованої координати x ₂= dx ₁/ dt.

Якщо права частина диференціального рівняння фазової траєкторії (3.9) є складною функцією, що утрудняє одержання рішення, наприклад, методом поділу змінних, то побудова фазової траєкторії можна зробити методом ізоклін.

Ізокліною – називається геометричне місце крапок у фазовій площині, для яких нахил дотичної до фазової траєкторії постійний, ті. дотримується співвідношення:

(3.10)

Тоді, задаючи значення С _і можна визначити рівняння ізокліни для кожного конкретного значення С _і із заданого ряду від +∞, до -∞.

що дозволить після побудови ізоклін нанести на кожну з них серію коротких відрізків однакового нахилу, обумовленого величиною С _і α = arctg C_i.

По заданих початкових умовах наноситься зображувана крапка М на фазовій площині і відповідно до напрямку стрілок на ізоклінах проводиться фазова траєкторія від ізокліни до ізокліни так, щоб криволінійні ділянки фазової траєкторії в крапках перетинання з ізоклінами мали нахил, що збігається з нахилом нанесеної серії коротких відрізків. Чим частіше нанесені ізокліни, тем точніше побудова.

Рис. 13 Фазова площина (x ₁, x ₂) і фазова траєкторія,

побудована методом ізоклін

Напрямок розвитку фазової траєкторії вказується написаними на ній стрілками. Справедливо наступне правило визначення напрямку руху (рис.13):

– у верхній півплощині крапка, що зображує, переміщається по фазовій траєкторії ліворуч праворуч, тому що всі значення х у цій області більше нуля що відповідає позитивному збільшенню самої координати x ₁.

– у нижній півплощині крапка, що зображує, переміщається по фазовій траєкторії праворуч ліворуч, тобто убік зменшення значень координати, тобто тому що в цій області значення швидкості x ₂ негативно:

– вісь абсцис перетинається з фазовими траєкторіями під прямим кутом, оскільки швидкість x ₂ для всіх крапок, що лежать на осі абсцис, дорівнює нулю, що вказує на мінімальне або максимальне значення координат х ₁. Слід зазначити, що це правило не дотримується для загального випадку рівняння (3.9).

Вид фазової траєкторії повністю визначає характер руху системи, тобто перехідний процес, що протікає в системі. Загасаючі коливальні процеси характеризуються тим, що кожне наступне значення максимального відхилення керованої координати від, що встановилося значення (перерегулювання) менше попереднього, отже, на фазовій площині такий процес зображується збіжною спіралеподібною фазової траєкторії. Розбіжні коливальні процеси, у яких картина зміни перерегулювання із часом зворотна, на фазовій площині зображуються розбіжною спіралеподібною кривою. Очевидно, що незатухаючий періодичний процес на фазовій площині буде представляти замкнену криву.

Монотонні перехідні процеси у фазовій площині зображуються у вигляді кривих, що монотонно наближаються (для загасаючих перехідних процесів) до положення рівноваги або, що монотонно віддаляються (для розбіжних процесів) від рівноважного положення, тобто початку координат фазової площини.

Постановка завдання оптимального керування включає: модель об'єкта керування, обмеження на керування та стан, початковий і кінцевий стан, функціонал якості керування. Потрібно знайти керування, що переводить об'єкт із початкового стану в кінцевий та мінімізуючий функціонал якості (критерій керування).

По вигляду функціонала якості розрізняють системи:

1) оптимальні по швидкодії:

2)

3) оптимальні по витраті ресурсів:

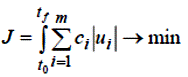
4) з мінімальною енергією керування:

5) з мінімальними втратами керування:

Можуть застосовуватися комбіновані функціонали якості.

«Конструювання» таких функціоналів є складною і у багато в чому певним завданням, ефективний метод рішення якої полягає в застосуванні моделювання.

Розглянемо двокритериальне завдання оптимального керування об'єктом з подвійним інтегруванням [4].

Нехай рівняння об'єкта має такий вигляд:

де x ₁, x ₂ – змінні стани; u – керування.

Задані початкові стани x ₁(0) = x ₁⁰, x₂ (0) = x₂⁰; кінцеві стани x ₁(T) = x₂ (T) = 0, де T – невідомий час переходу; обмеження на керування |u(t)| ≤ 1. Функціонал якості являє собою зважену суму двох функціоналів:

де J ₁ – функціонал якості систем оптимальних по швидкодії;

J ₂ – функціонал якості систем оптимальних по витраті ресурсів;

k – у загальному випадку невідомий позитивний ваговий коефіцієнт.

Відомо, що сформульоване завдання має рішення в замкненому виді. Структурна схема системи оптимального керування представлено на рисунку 14.

Коефіцієнт qk визначається за формулою:

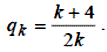
Мета подальших досліджень – вибір такого значення k, при якім досягається компроміс між швидкодією системи та втратами на керування.

Рис. 14. Структурна схема системи оптимального керування

Дійсно, якщо прийняти k = 0, то J = J ₂ і система стає оптимальною по витраті ресурсів, причому J ₁ у даному випадку може бути як завгодно більшим; якщо прийняти k → ∞, те «вага» функціонала якості J ₁ необмежено зростає, а функціонала якості J₂ необмежено зменшується, отже система стає оптимальною по швидкодії, хоча можлива значна втрата ресурсів на керування. Деяке «середнє» значення k може дати задовільне керування як по швидкодії, так і по витраті ресурсів.

Дата добавления: 2015-10-24