Порядок виконання роботи. Ідентифікація та моделювання

Ідентифікація та моделювання

Об’єктів автоматизації

Методичні вказівки до виконання лабораторних занять

для студентів спеціальності /7.092501/

«Автоматизоване управління технологічними процесами»

денної, заочної форми навчання та ФПС

Редакційно-видавничий відділ

Луцький національний технічний університет

Луцьк – 2011

УДК 621.325.5:621.382.049.77

ББК 34.5

Методичні вказівки до виконання лабораторних занять з курсу «Ідентифікація та моделювання ТП і ОА» для студентів денної та заочної форми навчання спеціальності /7.092501/ «Автоматизоване управління технологічними процесами» / С.С. Костєлов – Луцьк: ЛНТУ, ФКНІТ, АУВП, 2011 р. – 72 с.

Укладач: С.С. Костєлов

Рецензент: О.Ю. Повстяной

Відповідальний за випуск: Л.О. Гуменюк

Затверджено науково-методичною радою ЛНТУ,

протокол № ______ від_________ 2011 р.

Рекомендовано до друку методичною комісією

факультету КНіІТ,

протокол № ______ від__________ 2011 р.

Розглянуто на засіданні кафедри автоматизованого

управління виробничими процесами,

протокол № ______ від________ 2011 р.

Зміст

Вступ............................................................................................................... 4

Лабораторна робота №1................................................................................... 5

Лабораторна робота №2................................................................................... 14

Лабораторна робота №3................................................................................... 24

Лабораторна робота №4................................................................................... 35

Лабораторна робота №5................................................................................... 48

Лабораторна робота №6................................................................................... 58

Список використаних джерел.......................................................... 69

Вступ

Ідентифікація та моделювання технологічних об’єктів – це науково-технічна дисципліна, що займається питаннями побудови моделей об'єктів керування та систем керування і вирішує проблему оцінки параметрів цих моделей.

Формування моделей на основі результатів спостережень і дослідження їхніх властивостей – це, власне кажучи, і є основний зміст даної науки. Моделі ("гіпотези", "закони природи", "парадигми" і т.д.) можуть бути більш-менш формалізованими, але всі вони володіють тією головною особливістю, що зв'язують спостереження в якусь загальну картину. Рішення завдання побудови математичних моделей динамічних систем за даними спостережень за їхнім поводженням становить предмет теорії ідентифікації, що тим самим стає елементом загальної наукової методології.

А оскільки ми "оточені" динамічними системами, методи ідентифікації систем мають широкі додатки. Мета даних вказівок полягає в тім, щоб дати уявлення про наявні методи ідентифікації, їхньому обґрунтуванні, властивостях і застосуванні та показати практичне дослідження технологічних систем.

В процесі виконання лабораторних робіт, при розгляді проблеми ідентифікації необхідно буде виділяти статичний підхід та динамічний підхід до аналізу технологічних систем та об’єктів.

Сутність статичного підходу полягає в наступному: ставляться експериментальні дослідження, одержують експериментальну вибірку, що характеризує динаміку моделі, на підставі апріорних даних про фізичні процеси в моделі визначається структура самої моделі, а по експериментальній вибірці визначаються налагоджуючі параметри моделі.

Сутність динамічного підходу має деяку відмінність і полягає в наступному: є деяка замкнута система, у цій системі спеціальним чином вводиться додатковий контур ідентифікації, що відслідковує зміну параметрів моделі в процесі реального функціонування системи, на підставі деякого критерію робимо оцінку моделі і при необхідності змінюємо налагоджуючі параметри об'єкта, або системи в цілому.

Отже в процесі виконання лабораторних робіт ви зможете вивчити та застосувати на практиці методи побудови моделей для об'єктів систем керування та методи визначення динамічних параметрів цих моделей.

Лабораторна робота № 1

Оцінка якості перехідних процесів лінійних об'єктів і

Систем керування

Мета роботи: вивчення взаємозв'язків між прямими й непрямими показниками якості перехідного процесу.

Зміст роботи

При оцінці якості перехідного процесу лінійних об'єктів і систем керування використовуються як прямі, так і непрямі показники [1]. До прямих – ставиться ряд показників, одержуваних безпосередньо по перехідному процесу. До основних – час регулювання й перерегулювання, тому що перехідний процес ставиться до тимчасових динамічних характеристик. У такому випадку для одержання тимчасових характеристик системи застосовуються наступні типові впливи, що подається на вхід системи: одиничний східчастий вплив I (t), що представляє собою функцію часу, рівну нулю при будь-яких t менших нуля й рівну одиниці при значеннях t більших або рівних нулю (рис. 1).

Рис. 1. Одинична східчаста функція й дельта-функція

Зв'язок між розглянутими типовими впливами визначається наступними співвідношеннями:

Перехідна функція системи являє собою реакцію системи на вхідний вплив у формі одиничного східчастого сигналу (рис. 2).

Рис. 2. Ілюстрація до одержання перехідної функції: а – модель системи,

б – графіки сигналів

Час регулювання t_p – це мінімальний час, після закінчення якого регульована величина h (t) буде залишатися близької до значення, що встановилося, h _уст із заданою точністю Δ (звичайно 3-5% від h _уст), тобто:

Перерегулювання σ – максимальне відхилення перехідного процесу h _max від значення, що встановилося, h _уст, виражене у відсотках:

Прямі показники якості перехідного процесу не завжди зручні при синтезі системи. У цьому змісті більш кращі непрямі показники, які в основному орієнтовані на той або інший метод синтезу. Прикладами непрямих показників якості є кореневі частотні. Кореневі показники ґрунтуються на розташуванні кореня характеристичного рівняння замкненої системи в площині коренів. До них зіставляються: ступінь стійкості η – відстань від уявної осі до найближчого кореня, і коливальність μ – тангенс кута, утвореного від’ємною дійсною піввіссю й променем з початку координат до кореня, у якого відношення уявної частини до дійсної максимальне:

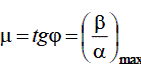
де β – уявна частина корінь характеристичного рівняння; α – дійсна частина.

Прикладом непрямої оцінки якості систем автоматичного керування по розташуванню коренів у площині коренів використовують метод кореневого годографа.

Кореневим годографом – називається траєкторія руху кореня характеристичного рівняння замкненої системи при зміні якого-небудь параметра системи, найчастіше коефіцієнта підсилення, від 0 до +∞.

Розглянемо динамічну систему, передатна функція якої в розімкнутому вигляді записується так:

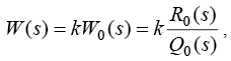
(1.1)

де k – коефіцієнт підсилення.

При одиничному негативному зворотному зв'язку передатна функція замкненої системи матиме вигляд:

(1.2)

Як видно по характеру полінома знаменника передатної функції замкненої системи при зміні коефіцієнта підсилення від 0 до +∞ коефіцієнти полінома D (s) будуть змінюватися, отже, коріння рівняння D (s)=0 також будуть змінювати своє положення в площині кореня, описуючи при цьому певні траєкторії. В загальному випадку для рівняння, що має дійсні коефіцієнти, коріння можуть бути дійсними або комплексно-сполученими. Отже, положення кожного кореня в площині, корінь для будь-якого значення змінюваного k буде визначатися вектором, характеризуючим модулем і аргументом. Тоді для полінома D (s)=0, представленого у формі 1+ W (s)=0, можна записати так: W (s)= –1.

Це рівняння можна представити у формі двох рівнянь:

рівняння модулів:

(1.3)

і рівняння фаз:

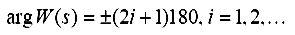
(1.4)

Ці два рівняння є основою для побудови кореневого годографа, оскільки кожна крапка кореневого годографа повинна задовольняти рівнянню модуля й рівнянню фаз.

Для побудови кореневого годографа зручно скористатися його властивостями, що випливають із рівняння модулів і рівняння фаз. Розглянемо найбільш важливі властивості кореневого годографа:

1. Початок кореневого годографа замкненої системи збігається з положенням полюсів розімкнутої системи, тому що при k =0 D (s)= Q (s).

Наприклад, для системи з передатною функцією в розімкнутому вигляді:

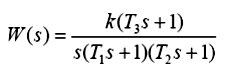
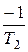нулі й полюси визначаються як P₁=0, Р₂= , Р₃= , N₁= (рис. 3).

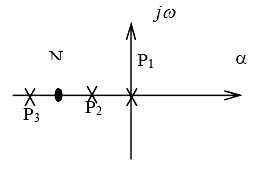
Рис. 3. Розташування нулів і полюсів передатної функції

2. Кореневий годограф має властивість безперервності й симетрії щодо дійсної осі. Безперервність годографа випливає з того, що при безперервній зміні коефіцієнта підсилення будуть безупинно змінюватися коефіцієнти характеристичного рівняння, що, у свою чергу, викличе безперервна зміна значення корінь, що описувало траєкторії на площині. Симетричність кореневого годографа щодо осі абсцис випливає із симетричності розташування комплексно-сполученого корінь щодо осі абсцис для кожного значення коефіцієнта підсилення k у межах від 0 до +∞.

3. Дійсна вісь площини корінь є ділянками кореневого годографа в тих її крапках, праворуч від яких розміщена загальна непарна кількість нулів і полюсів.

4. Кількість гілок кореневого годографа дорівнює порядку системи, причому m гілок, починаючись у полюсах, закінчуються в нулях (m – порядок чисельника), а інші n – m гілок ідуть у нескінченність. Гілки, що йдуть у нескінченність, асимптотично наближаються до напівпрямих, що називаються асимптотами кореневого годографа. Число таких асимптот n – m.

5. Крапка виходу асимптот лежить на дійсній осі, її положення визначається координатою σ_a, а кути нахилу асимптот - значеннями ϕ_ai:

Якщо кількість асимптот більше двох, то їх гілки спрямовані в протилежну сторону.

6. Якщо кореневий годограф лежить на дійсній осі і утворений двома полюсами, що вказує на зустрічний рух полюсів при зміні коефіцієнта підсилення, то при деякому значенні коефіцієнта, полюси збігаються, тобто утворюється кратний полюс. Подальша зміна коефіцієнта підсилення приведе до появи комплексно-сполученого кореня, тобто кореневий годограф виходить із дійсної осі і його гілки направляються в протилежні сторони. Крапка виходу кореневого годографа з дійсної осі може бути визначена на підставі рівняння фаз. Для цього не обходжене продиференціювати це рівняння й перейти від похідної до збільшень.

Тому що кути малі, те, з'єднавши крапку, що приблизно належить кореневому годографу, з усіма полюсами й нулями, можна для прямокутних трикутників записати рівняння збільшень через тангенси кутів, тоді:

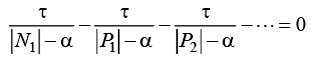
Скоротивши на τ і розв'язавши рівняння відносно α, знайдемо координату крапки виходу кореневого годографа з дійсної осі (рис.4).

Рис.4. Визначення крапки виходу кореневого годографа з дійсної осі

7. Кут виходу кореневого годографа з комплексно-сполученого кореня визначається на підставі рівняння фаз:

Розташовуючи кореневим годографом, можна для конкретного значення коефіцієнта підсилення вказати розташування кореня на комплексній площині й по ньому судити про якість системи у випадку простих початкових умов. При наявності полюса на початку координат або у випадку наближення дійсного полюса до початку координат процеси в системі стають більш повільними, отже, швидкодія системи знижується. Така ж поведінка нуля приводить до того, що у зв'язку із проявом форсування процеси прискорюються, але разом з тим зростають перерегулювання й коливальність, а це в остаточному підсумку збільшує час регулювання. Наближення полюса до нуля приводить до компенсації полюса нулем, що відповідає зниженню порядку системи. Характер перехідного процесу найбільшою мірою визначається полюсами, найбільше близько розташованими до уявної осі, тобто так званими домінуючими полюсами. Наближення будь-якого полюса до домінуючого полюса збільшує час перехідного процесу й перерегулювання.

Частотні показники якості обчислюються по частотних характеристиках системи.

Одержання частотних характеристик пов'язане із застосуванням у якості вхідного впливу типового сигналу гармонійного вигляду з одиничною амплітудою: , . При подачі на вихід синусоїдального гармонійного сигналу одиничної амплітуди на виході лінійної системи виходить також гармонійний сигнал тієї ж частоти. Причому якщо робити зміну частоти вхідного сигналу від 0 до ∞, через якісь інтервали, то для кожного значення частоти амплітуда вихідного сигналу буде змінюватися, крім того, буде змінюватися і зсув фази вихідного сигналу щодо фази вхідного сигналу. Ці явища й приводять до поняття частотних характеристик. Найбільш загальної з них є комплексна частотна характеристика.

Комплексною частотною характеристикою (КЧХ) системи – називається залежність відносної комплексної амплітуди вихідного гармонійного сигналу системи від частоти вхідного сигналу. Якщо вхідний і вихідний сигнали представити в тригонометричній формі запису як:

(1.5)

то КЧХ системи відповідно до визначення буде мати вигляд:

(1.6)

КЧХ легко отримати аналітично по передатній функції системи, шляхом вводу замінної s→jω. При такій заміні відбувається відображення уявної осі площини коренів у площину КЧХ у формі годографа комплексної частотної характеристики.

Розглянемо отриману КЧХ по передатній функції.

Комплексна частотна характеристика може бути представлена як в алгебраїчній формі W (jω)= U (ω)+ jv (ω), так і в тригонометричній:

(1.6)

де А (ω) – амплітудна, а φ(ω) – фазочастотна характеристики.

(1.6)

Амплітудно-частотною характеристикою (АЧХ) системи – називається залежність відносної зміни амплітуди вихідного сигналу від частоти вхідного.

Фазочастотною характеристикою (ФЧХ) системи – називається залежність різниці фаз між вхідним і вихідним гармонійними сигналами від зміни частоти вхідного сигналу (рис.5):

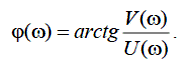
(1.9)

Рис. 5. Амплітудна частотна й фазова частотна характеристики

Поряд зі звичайними частотними характеристиками, широке застосування мають логарифмічні: амплітудна і фазова частотна характеристики (ЛАЧХ, ЛФЧХ), одержувані шляхом логарифмування вираження КЧХ, представленої в показовій формі.

Показник коливальностіM – це відношення максимального значення АЧХ замкненої системи до її значення при частоті ω=0. Частота зрізу ω _{с р} – частота, при якій АЧХ системи ухвалює значення рівне 1. Запас стійкості по фазі – величина кута , де φ(ω) – ФЧХ розімкнутої системи; ω _{с р} – частота зрізу розімкнутої системи. Запас стійкості по амплітуді – величина відрізка осі абсцис , укладеного між критичною крапкою (-1, j 0) і КЧХ розімкнутої системи.

Стійкість систем є необхідною умовою їх працездатності. Під стійкістю системи розуміють здатність динамічної системи вертатися у вихідний стан після зняття зовнішнього впливу або зберігати змушений рух, що відповідає дії зовнішньої сили, що обурює. Стійкість системи можна визначити за допомогою критеріїв стійкості Ляпунова, Гурвіца, Найквіста і Михайлова.

Частотні і кореневі показники якості пов'язані із часом регулювання та перерегулюванням. Однак аналітична залежність між ними в загальному випадку не встановлена і на практиці використовуються в основному наближені формули та моделювання.

Порядок виконання роботи

1. Визначите відрізок стійкості замкненої системи щодо коефіцієнта k, передатні функції задано в таблиці 1. При обчисленнях використовуйте не менш двох критеріїв стійкості.

2. Підбираючи коефіцієнт підсилення k, отримайте та зафіксуйте аперіодичний, монотонний, коливальний і нестійкий перехідні процеси в замкненій системі.

3. В програмному середовищі Matlab розробіть алгоритм обчислення прямих, частотних і кореневих показників якості.

4. Змінюючи коефіцієнт підсилення k у межах відрізка стійкості, для кожного перехідного процесу обчисліть прямі і непрямі показники якості. За результатами обчислювального експерименту побудуйте графіки наступних функціональних залежностей:

Таблиця 1.1

Передатні функції досліджуваних систем

Варіант	Передатна функція	Варіант	Передатна функція
1.		6.
2.		7.
3.		8.
4.		9.
5.		10.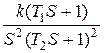

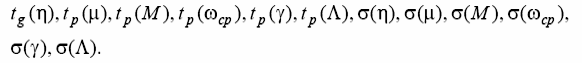
Зробіть висновки про взаємозв'язок показників якості перехідного процесу.

Зміст звіту

Звіт повинен містити: необхідні розрахунки по пп. 1-3; аперіодичний, монотонний, коливальний і нестійкий перехідні процеси; експериментальні функціональні залежності між прямими і непрямими показниками якості; висновки.

Контрольні питання

1. Поясніть різні методи побудови перехідного процесу систем автоматичного керування.

2. Дайте визначення частотним характеристикам лінійних систем автоматичного керування.

3. Що називається показником якості перехідного процесу? У чому відмінність між прямими і непрямими показниками?

4. Поясните характер залежності кореневих і прямих, частотних і прямих показників якості перехідного процесу.

Дата добавления: 2015-10-24