Решение задач 212—223 из учебника

Задача 212. Решений здесь имеется два. Поскольку условием не определяется только место совы в цепочке — она может быть первой или последней. Оставшаяся часть цепочки определяется однозначно: синица — попугай — орёл — курица — петух — сорока.

Задача 213. Здесь мы предлагаем детям решить задачу, аналогичную задаче 208, только не о днях недели, а о месяцах. Это практическая задача, поскольку она использует разговорную лексику, однако эта лексика имеет аналоги в нашем курсе. Так языковое выражение «через месяц» аналогично понятию «следующий месяц» в нашем курсе, а выражение «месяц назад» аналогично понятию «предыдущий месяц».

Задача 214. Здесь поиск приходится вести среди всех слов нашего Словаря. Первое утверждение проверять проще, чем второе. Поэтому стоит вести поиск всех слов с последней буквой А. Среди таких стоит выделять слова, в которых есть буква Я, и для них внимательно проверять второе утверждение. Итак, начинаем перебор с первого слова. Первое слово с последней буквой А — АНГИНА, но в нём нет буквы Я, поэтому пропускаем его. Точно такая же ситуация со словами: АПТЕКА, БЕЛКА, БУКВА, БУТЫЛКА и т. д. Первое по счёту слово с последней буквой А, в котором есть буква Я, — слово НЯНЬКА. Для него проверяем второе утверждение, видим, что оно истинно. Значит, мы уже нашли нужное слово. Заметим, что в Словаре такое слово единственное.

Задача 215 (необязательная). Конечно, эта задача имеет ровно одно решение. Поскольку в русском языке всего 10 гласных букв, именно они и должны лежать в искомом мешке.

Задача 216 (необязательная). Эта довольно сложная задача взята из обыденной жизни, окружающей второклассника. Для детей, в большей степени включённых в реальную жизнь (благодаря самостоятельности или своевременной помощи родителей), задача может оказаться совсем простой. Детей с «чисто академическими» знаниями (таблица умножения и куча стихов наизусть) эта задача может поставить в тупик. Вероятно, некоторые не поймут смысл вывески универмага. Объясните им, что квадратики справа означают дни недели: синие соответствуют рабочим дням, красный — выходному. Если ребёнок не может догадаться сразу, какой день выходной, пусть сосчитает синие квадратики и дни недели.

Ответ: первое, третье и последнее утверждения истинные, остальные — ложные.

Задача 217 (необязательная). В целом эта задача сложная — окон много, а информации очень мало; кроме того, есть несколько ловушек. Для начала нужно выделить утверждения, которые можно использовать сразу (то есть те, в которых речь идёт о станциях, уже помеченных на схеме). Здесь ребята сталкиваются с первой интересной особенностью задачи — в условии есть утверждения, которые уже истинны, поэтому их нужно сразу пометить (они нам не пригодятся) — это четвёртое и седьмое утверждения. Теперь найдём условия, которые можно использовать сразу — это третье, предпоследнее и последнее утверждения. В результате мы поместили в схему станции: Тверская, Театральная и Коломенская (заметим, что шестое утверждение при этом становится истинным автоматически). Теперь прочтём первое, второе и пятое утверждения. Конструкции «вторая после» и «вторая перед» говорят о том, что станции: Аэропорт, Сокол, Войковская и Динамо, мы должны поставить в четыре подряд идущих пустых окна. Правильную последовательность учащийся может получить в ходе проб и ошибок, в ходе сопоставления двух фрагментов (Войковская — Аэропорт, Сокол — Динамо) или в ходе одновременного анализа трёх утверждений. Главное, чтобы, обнаружив ошибку, ребёнок терпеливо вернулся к началу этого фрагмента и попробовал другой вариант. Наконец, у нас осталось одно пустое окно и одно утверждение, которое даёт нам название недостающей станции. Несмотря на то, что решение этой задачи вы, наверняка, доверите сильным ученикам, они вряд ли будут рассуждать столь чётко, да и не надо этого от них требовать. Однако приведённые здесь рассуждения помогут вам сдвинуть учащегося с мёртвой точки, не подсказывая ему решения. Посоветуйте детям сначала писать простым карандашом. И конечно, недопустимо, чтобы дети просто списывали решение со схемы линий метро.

Задача 218 (необязательная). Это не очень сложная задача, и многие дети решат её быстро. При этом большинство ребят слово просто угадают. Слабым учащимся можно подсказать, что это слово обозначает день недели. Вообще слов, обозначающих дни недели, из 11 букв всего два, поэтому перебор будет совсем не большим.

Задача 219 (необязательная). Утверждений в описании здесь достаточно много, но шаблоны для слов в цепочке однозначно определяют каждое слово, поэтому здесь невозможно зайти в тупик. Это означает, что если ребёнок смог (по окнам и буквам) вписать одно из слов, упоминаемых в утверждении, в цепочку, то сделал это правильно. Поэтому содержание данных утверждений можно было бы вообще не анализировать, а вписывать каждое слово просто туда, куда оно подойдёт. Но дети, конечно, заметят эту особенность не сразу, поэтому будут использовать утверждения достаточно активно.

Задача 220 (необязательная). Задача на повторение алгоритма подсчёта областей картинки. Эта задача не слишком сложная, её можно предложить практически любому ученику в классе.

Ответ: в этой картинке 6 областей.

Задача 221 (необязательная). Аналогичные задачи детям уже встречались (см. комментарии к задаче 207 из учебника).

Ответ: слово НАЧАЛО идёт в Словаре раньше слова НЕДЕЛЯ.

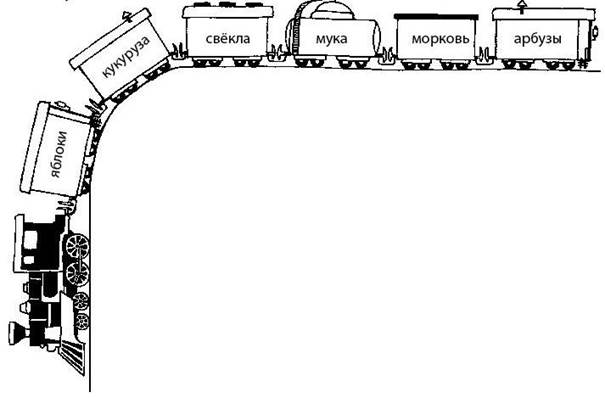
Задача 222 (необязательная). Естественно, начать решение учащийся должен с определения начала и конца цепочки. Потом стоит выделить и использовать те утверждения, которые определяют положение вагонов однозначно, так мы находим положение вагонов с мукой, а затем с морковью. Далее ребята могут пробовать разные варианты, имея в виду, что для свёклы и кукурузы необходимо найти два подряд идущих вагона.

Решение задачи:

Задача 223 (необязательная). В этой задаче дети повторяют понятие «каждый» и заодно вспоминают, что две симметричные фигурки в нашем курсе считаются разными.

Компьютерный урок «Выравнивание, решение необязательных и трудных задач»

Дата добавления: 2015-10-31