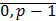Уравнение Эйлера
Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов | Поле направлений Изоклины. Особые точки, особые решения ДУ с разделяющимися переменными. | ДУ 1 порядка, однородные и сводящиеся к ним, ДУ в полных дифференциалах. | Имеющие одной из перменных. | Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы. | Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица. | Определение 1. | Следствие 4 | Часть доказательства. | Теорема о существовании непродолжаемого решения задачи Коши. |
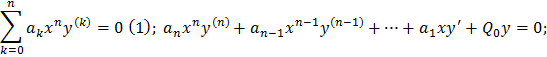
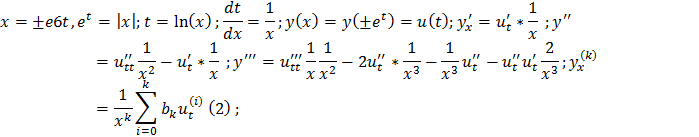
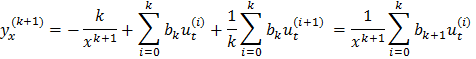
(2) оправдано при k=0 1, 2,3. При к произвольном следует его справедливость для k+1=>2 верно для любого 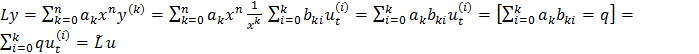
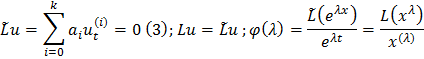
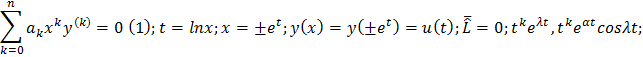
 (
(  )
) 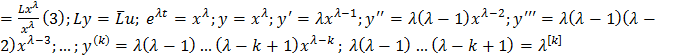
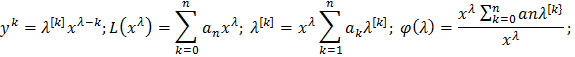
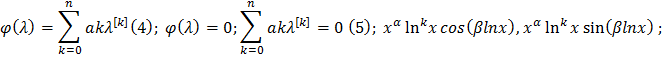
Если 𝜆 –действительный корень характерестического уравнения (5)б уравнениеЭйлера (1), кратности р, то ему соответсвует ФСР ур (1), соответсвует функции  k=
k= 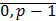 ; 𝜆=
; 𝜆= 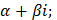
Характерестическое уравнение (5) в ФСР ур (1) соответсвует функц 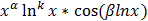
 ; k=
; k= 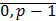
Дата добавления: 2015-09-01; просмотров: 67 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.008 сек.)

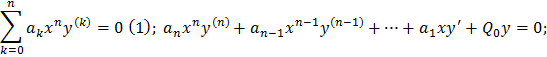
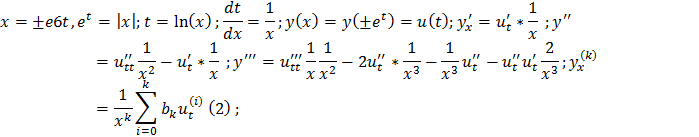
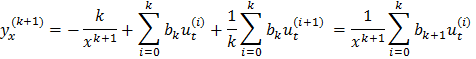
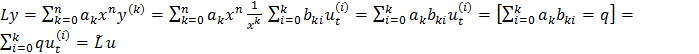
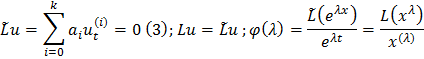
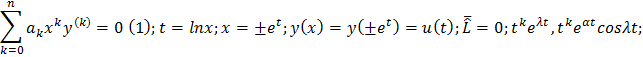
 (
(  )
) 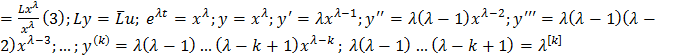
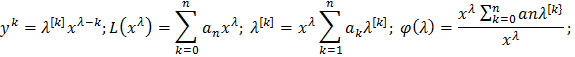
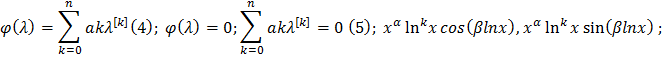
 k=
k= 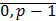 ; 𝜆=
; 𝜆= 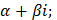
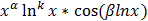
 ; k=
; k=