
Читайте также:
|
Система функций лин. Незваисима, если никакое их нетривиальная комбинация ЛК≢0 и линейно зависим в противном случае.
Система фектор функций называется Лин независимой в промежутке, если никкая Нетривиальная ЛК≢0 в этом промежутке.
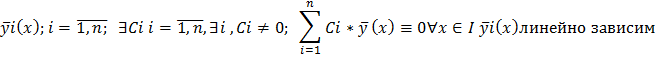
Система вектор – функций Л зависима в промежутке, Л Зависима в каждой точке.
Следствие. Если сист вектор. Функций л/независима хотя бы а 1 точке промежутка, то она л/независима и в промежутке.
Замечание Обратное для произвольных вектор функций неверно(касательно самого утверждения)
Теорема 1.
Множество решений ЛОДУ или СЛОДУ, есть линейное пространство.
Док-во.
Л.Операция, т е сложение и уножение на число вводятся обыч образом, как операции над функциями и вектор-функциями. Т к Диф(дифференцирование?) вектор-функция выполняется покоординатно,и лин. оператор так же, а линейный. опрер. над скаляр. функциями выполняются как операции над их числ. значениями, то эта операция обладает всеми свойствами сложения и умножения чисел. => для них выполняется все аксиомы ЛП(линейного пространства)
Теорема 2.
пространство U – изоморфно 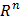
Док-во.
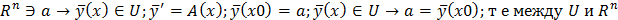
взаимооднозначное соответсвие. и при уножении на число начальный вектор умножают на число. т е 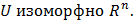
Дата добавления: 2015-09-01; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица. | | | Следствие 4 |