Читайте также:
|
Если функция f(x,y0,y1…yn-1) в открытой области R^n+1 непрерывна и обладает в ней непрерывностью 
пусть 
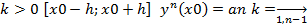
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале(a, b) производные 
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.
Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, После определения вида указанных постоянных и неопределенных функций решения становятся частными.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Говорят, что задача Коши имеет единственное решение, если она имеет решение 
и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки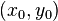 
имеет поле направлений, совпадающее с полем направлений . Точка 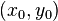задаёт начальные условия.
Каательная к функции, скорость-производная производная от координаты по времени есть скорость
ИЗОКЛИНА
обыкновенного дифференциального уравнения 1-го порядка
- множество точек плоскости х, у, в к-рых наклон направлений поля, определяемого уравнением (*), один и тот же. Если к- произвольное действительное число, то k-изоклина уравнения (*) есть множество
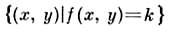
Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Дата добавления: 2015-09-01; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов | | | ДУ 1 порядка, однородные и сводящиеся к ним, ДУ в полных дифференциалах. |