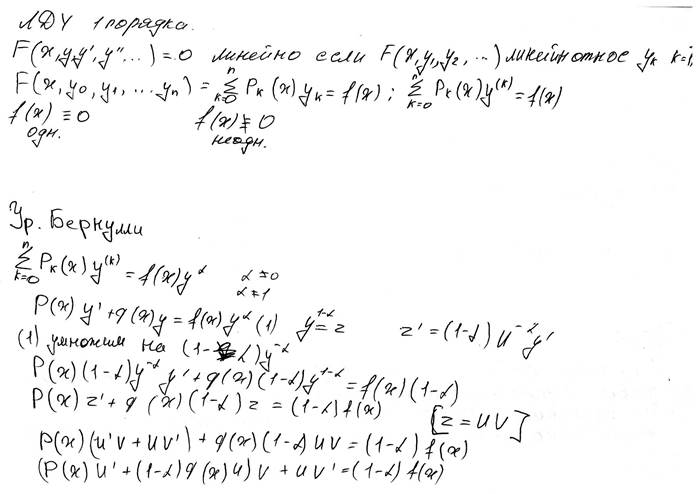Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

ДУ 1 порядка, однородные и сводящиеся к ним, ДУ в полных дифференциалах.

Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов | Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы. | Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица. | Определение 1. | Следствие 4 | Системы ЛДУ с постянными коофицентами. | Уравнение Эйлера | Функция Коши. Ее построение по ФСР. | Часть доказательства. | Теорема о существовании непродолжаемого решения задачи Коши. |


Читайте также:
  1. D-изображения. Геометрия проецирования. Однородные координаты.
  2. АЛЬТЕРНАТИВНЫЕ ПОДХОДЫ К АНАЛИЗУ ПОЛНЫХ ТАБЛИЦ
  3. КВАЗИНЕЗАВИСИМОСТЬ И ДРУГИЕ МОДЕЛИ ДЛЯ НЕПОЛНЫХ ТАБЛИЦ
  4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
  5. Меню для полных
  6. Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица.

Линейные ДУ 1-го порядка, уравнения Бернулли.

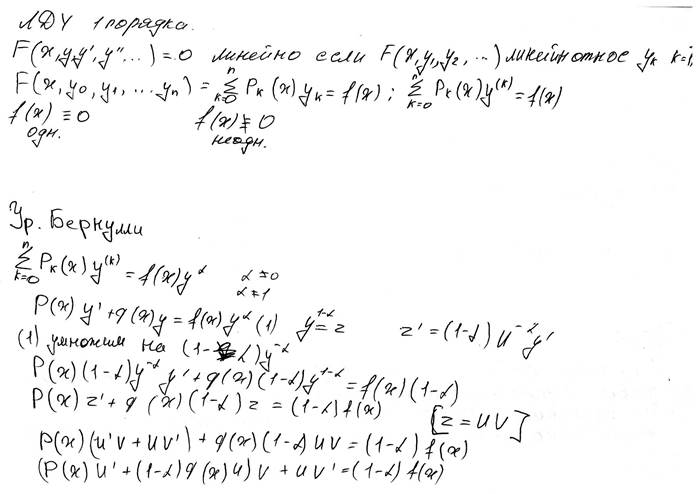
ДУ не разрешенные относительно производной, уравнения разрешенные относительно одной из переменных. Уравнение Лагранжа и Клеро.

Лагранж и клеро далее.

ДУ не разрешимые относительно производной. Уравнения не

Дата добавления: 2015-09-01; просмотров: 93 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Поле направлений Изоклины. Особые точки, особые решения ДУ с разделяющимися переменными.| Имеющие одной из перменных.
mybiblioteka.su - 2015-2025 год. (0.005 сек.)