Системы ЛДУ с постянными коофицентами.
Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов | Поле направлений Изоклины. Особые точки, особые решения ДУ с разделяющимися переменными. | ДУ 1 порядка, однородные и сводящиеся к ним, ДУ в полных дифференциалах. | Имеющие одной из перменных. | Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы. | Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица. | Определение 1. | Функция Коши. Ее построение по ФСР. | Часть доказательства. | Теорема о существовании непродолжаемого решения задачи Коши. |
18. ЛОДУ Н-го порядка с постоянными коофицентами. Уравнения Эйлера.


 (2) (5) – ФСР сист 2 и 3
(2) (5) – ФСР сист 2 и 3
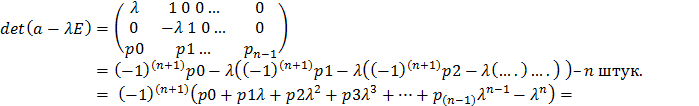
= 
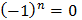
(𝜆)=0 (6); (𝜆)=𝜆^n- 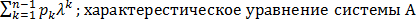
Ly 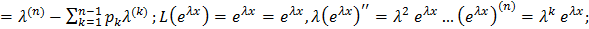
 =
= 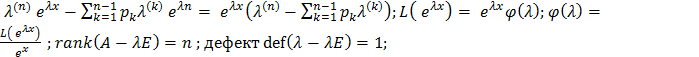
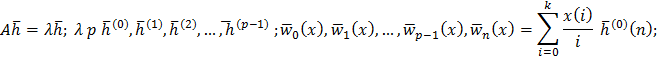
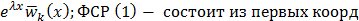
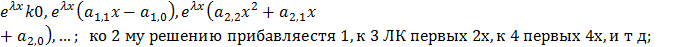
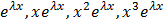
1 вывод
Если -корень характерестического уравнения ЛОДУ с постоянными коофицентами, кратности р, то ФСР ЛОДУ ему соответствует функция 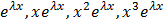 , если 𝜆-действительн переменнаяБ то все ОК
, если 𝜆-действительн переменнаяБ то все ОК
Если комплексная, то комплексному корню сооответсвует сопряженный корень.
Полученны пары комплексно-сопряженных решений.
Дата добавления: 2015-09-01; просмотров: 57 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.005 сек.)



 (2) (5) – ФСР сист 2 и 3
(2) (5) – ФСР сист 2 и 3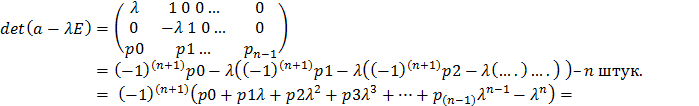

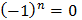
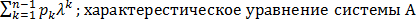
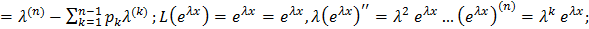
 =
= 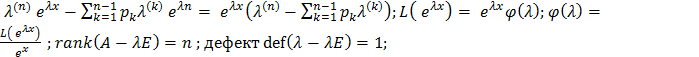
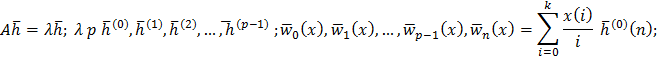
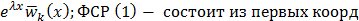
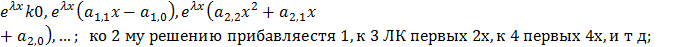
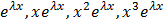
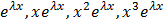 , если 𝜆-действительн переменнаяБ то все ОК
, если 𝜆-действительн переменнаяБ то все ОК