Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов

Задачи приводящие к дифференциальным уравнениям. Основные понятия. Задача Коши.

В различных областях науки и техники весьма часто встречаются задачи, для решения которых требуется решить одно или несколько уравнений, содержащих производные некоторых функций. Такие уравнения называются дифференциальными.
Задача 1. На плоскости хОу требуется найти кривую, проходящую через точку О (0; 0) и обладающую тем свойством, что угловой коэффициент касательной, проведенной в любой точке кривой, равен удвоенной абсциссе точки касания.

Пусть y = f (x) — уравнение искомой кривой. По условию, в каждой точке М (х; f (х)) имеется касательная к этой кривой, угловой коэффициент которой, т. е. f ' (x), равен 2 х.

Таким образом, (1) Это дифференциальное уравнение, так как оно содержит производную искомой функции.

Из уравнения (1) следует, что функция у есть первообразная функции 2 х. Поэтому или , (2)где С — произвольная постоянная. Из формулы (2) видно, что дифференциальное уравнение (1) имеет бесконечное множество решений.

Чтобы из этого множества решений выбрать искомое, надо воспользоваться тем, что искомая кривая проходит через точку О (0; 0). Следовательно, координаты этой точки должны удовлетворять уравнению (2), т. е. 0 = 0 + С, откуда С = 0. Итак, искомая кривая — это парабола .

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).

Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале(a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.

Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, После определения вида указанных постоянных и неопределенных функций решения становятся частными.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Говорят, что задача Коши имеет единственное решение, если она имеет решение и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки 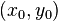имеет поле направлений, совпадающее с полем направлений . Точка 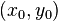задаёт начальные условия.

Теорема существования и единственности решения задачи Коши. Формулировка. Процесс Пикара. Доказательство его бесконечноти и непрерывности его элементов

Рассматривается задача Коши

X’= f(t, x),

(НС)

x(t0) = x0,

(НУ)

состоящая из нормальной системы (НС) и начального условия (НУ). Предполагается, что

(1)

функция f(t, x) непрерывна по t при любом фиксированном x;(2)

f(t, x) удовлетворяет по x условию Липшица с некоторой константой L:

(3)

Исследуется вопрос о существовании и единственности решения задачи (НС), (НУ) и изучается метод последовательных приближений для приближенного отыскания решения.

Последовательные приближения. Пусть

— произвольная непрерывная функция

(4)

Последовательные приближения, соответствующие начальному приближению j₀, определим с помощью рекуррентной формулы

(5)

Покажем индукцией по k, что при любом k определена на всем отрезке [ a, b ] и непрерывна. Для k = 0 это совпадает с (4). Пусть обладает указанными свойствами. Тогда в правой части (5) под интегралом стоит непрерывная на [ a, b ] функция — это следует из свойств j _k и условий (1) – (3). Поэтому также определена на [ a, b ] и дифференцируема, а следовательно, и непрерывна.

Итак, все последовательные приближения определены на [ a, b ] и непрерывны. Отметим еще, что из (5) вытекают два равенства

(6) и (7)

Формулировка теоремы Коши — Пикара. Пусть выполнены условия (1) – (3). Тогда:

1) задача (НС), (НУ) имеет на[a, b]единственное решениеj;

2) последовательные приближения (4), (5) сходятся на[a, b]кj, причем справедлива следующая оценка погрешности k-го приближения:

(8)

где

L ₂ = L ₁ e^c, L ₁ = ||j₀ – j₁||, c = L ·(b – a),

L — константа из условия Липшица (3).

Д о к а з а т е л ь с т в о будет состоять из четырех лемм.

2.3.4. Замечание о единственности. Из сформулированной теоремы вытекает следующее усиленное утверждение о единственности: если j и y — любые два решения задачи (НС), (НУ), определенные не обязательно на всем отрезке [ a, b ], то они совпадают на Действительно, если это не так, то найдется отрезок [a, b] на котором эти решения не тождественны. Но теорема Коши — Пикара, примененная на множестве [a, b] × R ⁿ, утверждает, что это невозможно.

Переходим к доказательству теоремы.

Лемма о существовании. В рассматриваемых условиях предел последовательных приближений jесть решение задачи (НС), (НУ).

Д о к а з а т е л ь с т в о. Заметим, что j¢_k(t) равномерно сходится

||j¢_k(t)– f[t, j(t)]|| = ||f[t, j_k–1(t)] – f[t, j(t)]|| £

£ L||j_k–1(t) – j_k(t)||.

Итак, j_k(t) ® j(t) при k ® ¥ и j¢_k(t)Þ j(t) при k® ¥ (t Î [a, b]). По теореме Вейерштрасса о дифференцировании функциональных последовательностей отсюда следует равенство j¢(t) = f[t, j(t)]. Кроме того, j(t₀) = lim_k®¥j_k(t₀) = x₀.

Лемма о сходимости. В условиях теоремы Коши — Пикара последовательные приближения равномерно на [ a, b ] сходятся к некоторой функцииj, причем

||jk - j|| £ L2

c^k k!

.

(15)

Д о к а з а т е л ь с т в о. Покажем, что последовательность {j_k} фундаментальна в C. Сначала оценим ||j_k – j_k+1||. Для этого применим лемму о сближении к начальным функциям j₀ и y₀ = j₁. Тогда, очевидно, y_k = j_k+1, L₀ = ||j₀ – y₀|| = ||j₀ – j₁|| = L₁ и, следовательно,

||jk – jk+1|| £ L1

c^k k!

.

Отсюда получаем оценку для ||j_k - j_p|| (p > k):

||j_k – j_p|| £

£ ||j_k – j_k+1|| + ||j_k+1 – j_k+2|| +... + ||j_{p – 1} – j_p|| £

£ L1

p – 1 å i = k

c^i i!

£ L1

¥ å i = k

c^i i!

£ L1

= L1Pk

(16)

где P_k ® 0 при k ® ¥ как остаток сходящегося ряда.

Итак, последовательность {j_k} фундаментальна, поэтому в силу полноты пространства C она сходится в норме этого пространства к некоторой функции j Î C. Для получения неравенства (15) оценим P_k:

Pk =

¥ å i = k

c^i i!

=

c^k k!

¥ å i = k

c^i–kk! i!

£

c^k k!

¥ å i = k

c^i–k (i – k)!

,

поскольку при i ³ k, очевидно, i! ³ k!(i – k)!. Введем теперь новую переменную суммирования j = i – k:

c^k k!

¥ å i = k

c^i–k (i – k)!

=

c^k k!

¥ å i = k

c^j j!

=

c^k k!

e^c.

Отсюда и из (16) предельным переходом при p ® ¥ получаем (15).

Лемма о единственности. В условиях теоремы Коши — Пикара решение задачи (НС), (НУ) на[a, b]единственно.

Д о к а з а т е л ь с т в о. Если j и y — решения этой задачи на [a, b], то построим последовательные приближения j_k, y_k, соответствующие начальным приближениямj₀ = j, y₀ = y. Из (6) и (7);(6), (7) в этом случае видно, что j_k = j, y_k = y при любом k. Но тогда из леммы о сближении следует, что j = y.

Доказательство теоремы Коши — Пикара завершено.

Дата добавления: 2015-09-01