Читайте также:
|
Функция Коши;См билет выше;
24. Метод неопрделенных коофицентов при в=0, они вместе там искать надо,
25 Метод неопрделенных коофицентов при в≠0
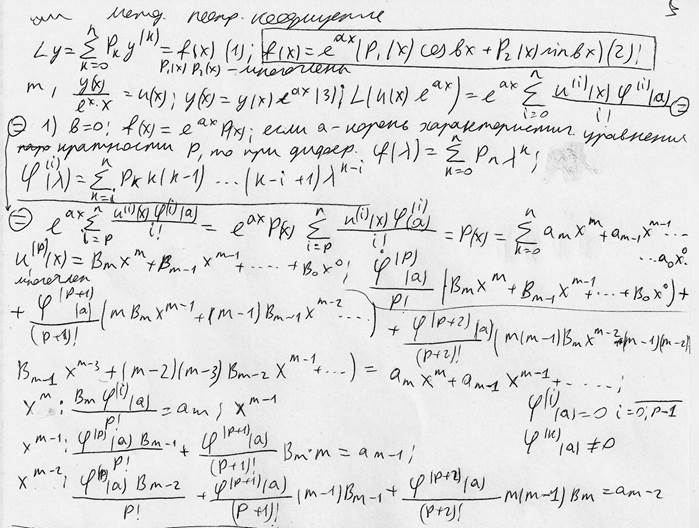
. придется интегрировать р-раз,пологая,при каж дом интегрировании пр-я=0;молучим многочлен с младшим членом 
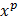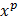, можно вынести.
; 
- многочлен степени n; ур 1 с прав частью 
; 
многочлен степени m; имеет частное решение вида 
-
p –кратность а; как корня характерестического уравнения.
Всё это пригодно и для комплексных чисел.
ЛНДУ со свобод. Вида 
имеет частное решение
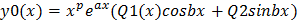p –кратность s=a+bi; как корня характерестического уравнения.
26. Продолжение решений ду, условие продолжимотти., непродолжаемые решения.
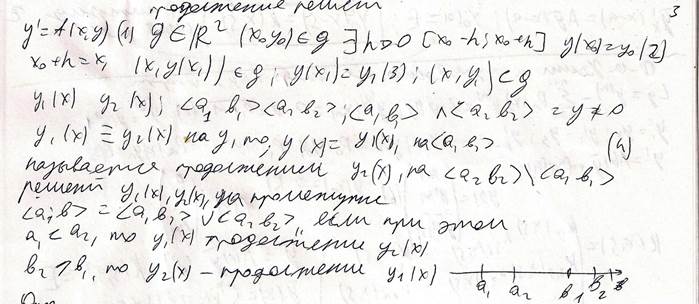
Опред: Решение y(x) ур(1) опр на <а, b >, называется непродолжающимся если не существует его продолжения y1(x) на <a,b> 
Дата добавления: 2015-09-01; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение Эйлера | | | Часть доказательства. |