Читайте также:
|
Теорема 3 Общее решение СОДУ есть ЛК ФСР с произволь. постоянными коофиуентами.
Док-во
пусть 
1. всякое ЛОДУ с непрерывными коофицентами имеент ФСР
2.Общее решение ЛОДУ есть ЛК его ФСР с произвольными коофицентами.
Т4 
Док-во
пусть 
частное решение 
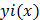; i=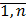 
– ФСР (8)тогда по 2му свойству разность 
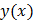ур 7 и y0(x)- есть решение 8; 
(при соответств)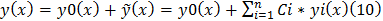 
(10)-содержит в себе все части решения уравнения (7) y(x)-при любых Ci является решенем (8)по свойству 3 y(x)=y0(x)+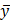 
(x) – решение 7; 10 при любых Ci –общее решение 7; y(x)- общ. решение 8ж так что обще реш 7, есть частное решение 8.
Дата добавления: 2015-09-01; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение 1. | | | Системы ЛДУ с постянными коофицентами. |