Читайте также:
|
Доказательство: Т.к.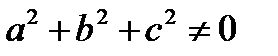 
то уравнение(22.2) имеет один корень (x0,y0,z0). ax+by+cz+d=0(22,3). Вычитаем (22,3) из (22,2)=> 
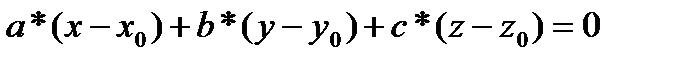А это и есть уравнение (22,1), которое определяет плоскость проходящую через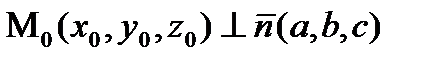 
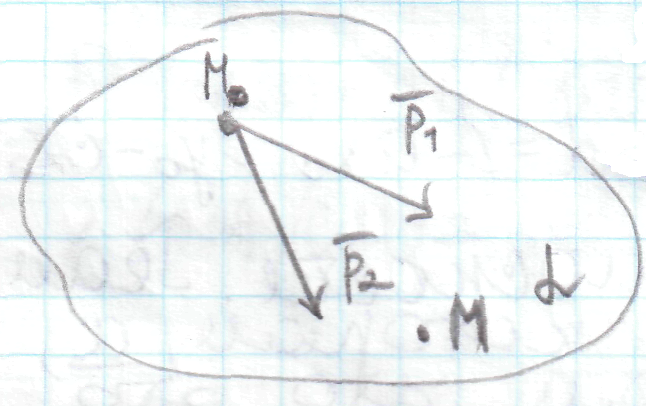
22.2 Уравнение плоскости, проходящей через M0,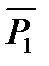 
, 
.
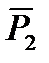α(M0, 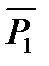, 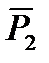), M0(x0,y0,z0), 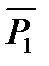(p1,p2,p3),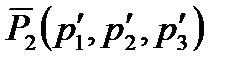 
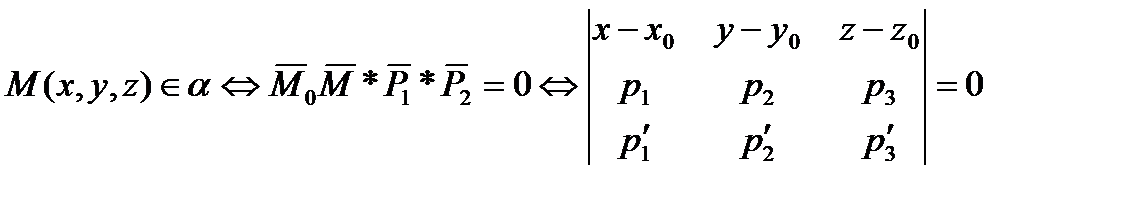(22,4)
22.3 Уравнение плоскости, проходящей через 3 точки.
α(M1, M2, M3), M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3)
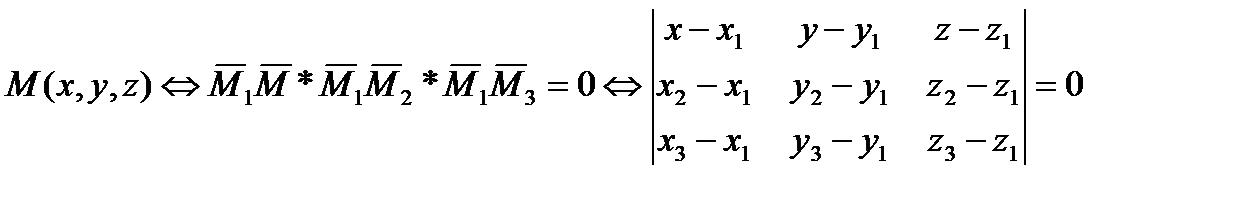(22,5)
Общий подход к решению задач: Плоскость.
1. Вычислите один из способов задания плоскости: 1) α(М0,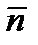 
) 2) α(M0, 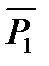, 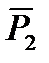) 3) α(M1, M2, M3)
2. Запишите уравнение, соответствующее выбранному способу:
1) 
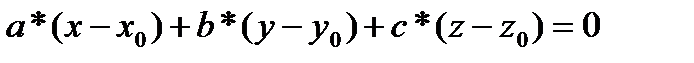
2) 
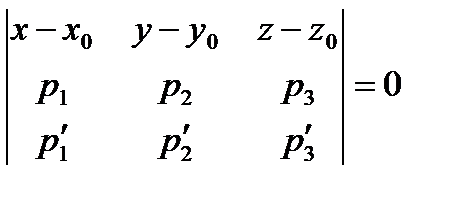
3) 
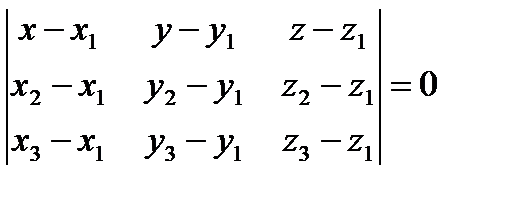
3. Запишите в общем виде.
ax+by+cz+d=0
Замечание: в решении задач на составление уравнений плоскостей, не всегда удается сразу найти способ задания плоскости, но часто для нее нахождение объектов, определяющих плоскость, помогают формулу вычисления расстояния от точки до плоскости и вычисление угла между плоскостями.
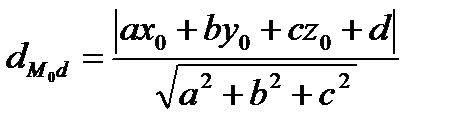
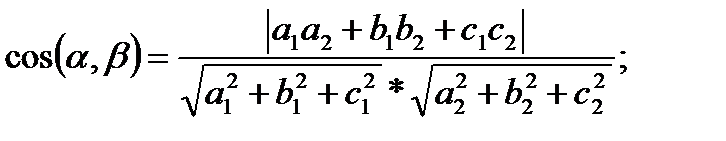
Дата добавления: 2015-09-05; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Различные способы задания плоскости в пространстве. Общий подход к решению задач на составление уравнений плоскости. | | | Прямая линия в пространстве. Различные способы задания прямой в пространстве и ее уравнения. Общий подход к решению задач на составление уравнений прямых |