Прямая линия в пространстве. Различные способы задания прямой в пространстве и ее уравнения. Общий подход к решению задач на составление уравнений прямых

Прямая в пространстве однозначно определяется заданием:

1. ее точки и направляющего вектора, l (М₀, )

2. двух ее точек, l (M₁,M₂)

3. двух плоскостей по которым она пересекается, l(α,β)

23.1 Уравнение прямой, заданной l (М₀, )

l (М₀, ), M₀(x₀,y₀,z₀), (p₁,p₂,p₃)

(23,1)-каноническое; (23,2)-параметрическое

23.2 Уравнение прямой, проходящей через М1, М2

l (M₁,M₂)

23.3 Уравнение прямой заданной двумя плоскостями

l(α,β), 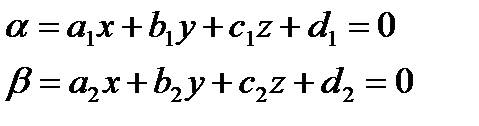(23,4) (23,4)- общее уравнение прямой

Рассмотрим переход от (23,4) к (23,1)

Пусть - направляющий вектор l,

В качестве точки M₀(x₀,y₀,z₀) можно взять точку одну из координат у которой можно взять произвольно, а две другие найдутся как решение системы.

Пример:

l(α,β),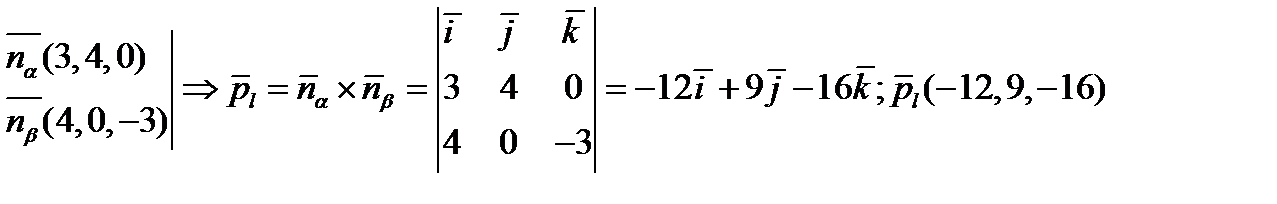

Пусть произвольная ;

Общий подход к решению задач: Прямая.

1. Выделите один из трех способов задания прямой.

а) l (М₀, )

б) l (M1,M2)

в) l(α,β)

2. Запишите уравнение, соответствующее выбранному способу

а)

б)

в)

3. Запишите уравнение в каноническом виде.

23.4 Вычисление расстояния от точки до прямой.

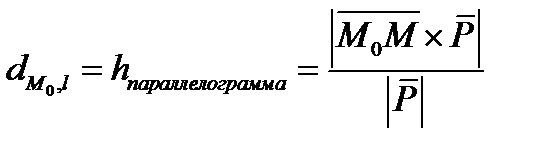
23.5 Вычисление расстояния между скрещивающимися прямыми

Параллелепипед: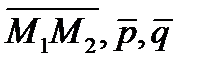

23.6 Нахождение угла

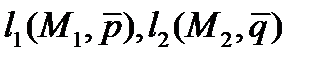
Пример: Составьте уравнение прямой

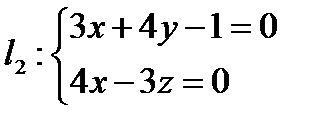
Дата добавления: 2015-09-05