Читайте также:
|
1. Через точку М(0,-1,1), провести прямую перпендикулярную прямой 
, 
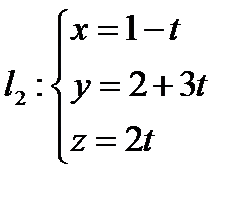1) 
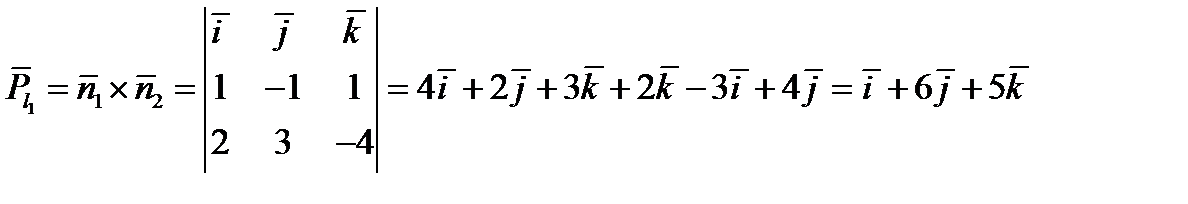
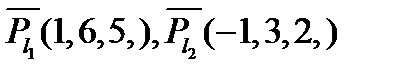
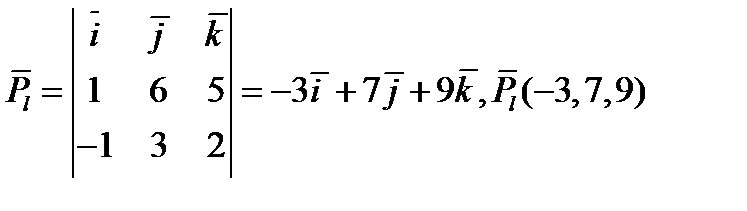
2) Записать уравнение
2. 
Составить уравнение прямой проходящей через М(0,-1,1) и пересекающие прямые l1 и l2.
, 
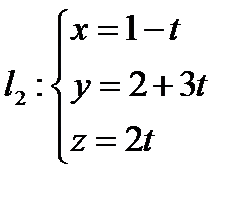
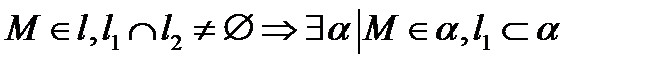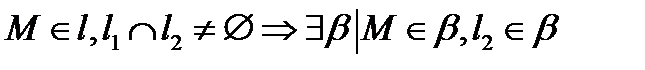
1) 
2) 
Пусть 
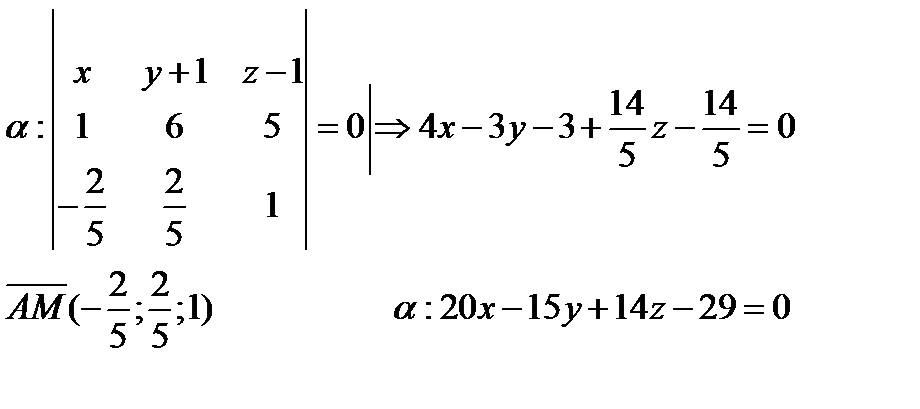
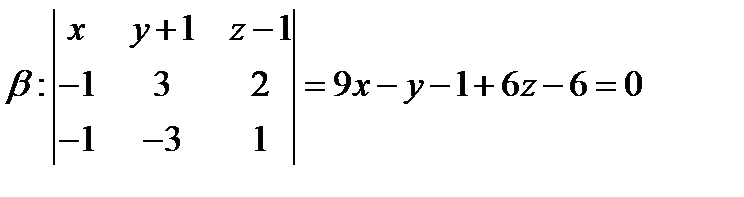
3) 
3. Составить уравнение прямой проходящей через М(0,-1,1), перпендикулярную l1 и пересекающую l2
1) 
l(α,β)
2) 
, 
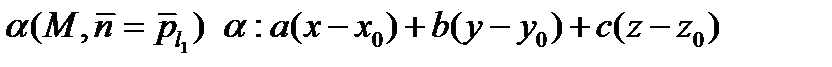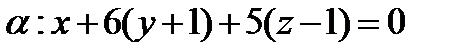
3) 
4. Даны две плоскости 
Составьте уравнение плоскостей, делящих двугранные углы этих плоскостей пополам.(Биссектриса плоскости)
Пусть δ- биссекторная плоскость, для α и β. δ= Г.М.Т.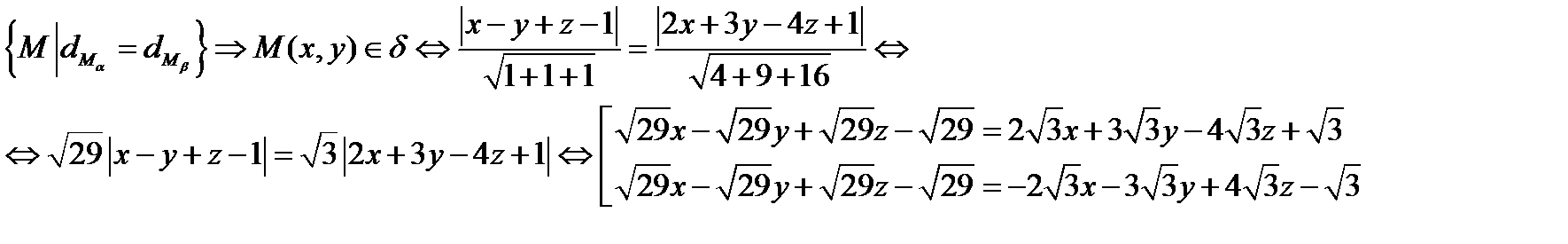 
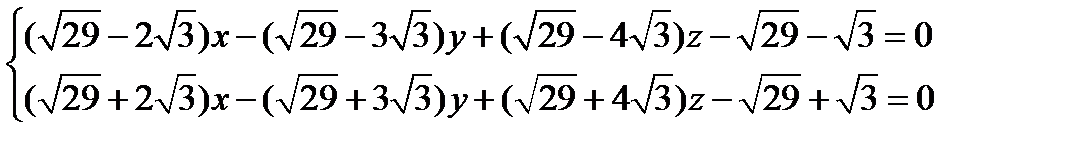
Дата добавления: 2015-09-05; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямая линия в пространстве. Различные способы задания прямой в пространстве и ее уравнения. Общий подход к решению задач на составление уравнений прямых | | | Деятельность профсоюзов России 1910-1914 гг. |