Различные способы задания плоскости в пространстве. Общий подход к решению задач на составление уравнений плоскости.

Прямые и плоскости в пространстве.

Плоскость в пространстве однозначно определяется заданием:

1. ее точки и нормального вектора перпендикулярного = α(М₀, )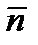

2. ее точкой и двумя направляющими векторами(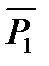 не параллельно 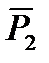, P₁и P₂ параллельно α)= α(M₀, , )

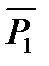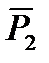3. Тремя ее точками M₁,M₂,M₃=α(M₁,M₂,M₃₎

22.1 Уравнение плоскости заданное точкой и нормальным вектором.

α(М₀, 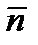) R(o, 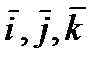) M₀(x₀,y₀,z₀) 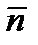(a,b,c)

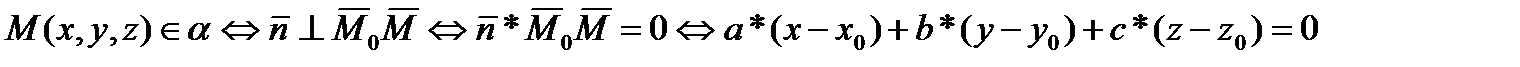(22,1)

(22,1)=> ax+by+cz+d=0, d=(-ax₀-by₀-cz₀) (22,2)

(22,2)- обще уравнение плоскости. Геометрический смысл коэффициентов, в котором, a, b и с состоит в том, что это и есть координаты.

Теорема (22.1)

Дата добавления: 2015-09-05