Читайте также:
|
Произведение векторов 
, когда два вектора 
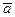и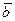 
множатся векторно, а результат их произведения (вектор 
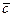) множится скалярно на вектор 
, называется смешанным или скалярно векторным произведением трех векторов.
Свойства смешанного произведения:
1. Координатная форма смешанного произведения представляет собой определитель третьего порядка, у которого последовательно по строкам стоят координаты векторов-сомножителей:
.
2. Операции скалярного и векторного умножения в смешанном произведении можно менять местами, а тогда знаки векторного и скалярного умножения в смешанном произведении можно опустить:
.
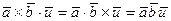При этом во втором случае, согласно определению смешанного произведения, сначала вектора 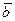и множатся векторно, а результат их произведения (вектор) множится на вектор 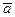скалярно.
3. При перестановке двух сомножителей в смешанном произведении оно меняет знак на противоположный, сохраняя абсолютную величину:
.
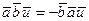Геометрический смысл смешанного произведения.
Абсолютная величина смешанного произведения трех векторов численно равна объему параллелепипеда, построенному на этих векторах:
.
Если перемножаемые векторы компланарны, то в параллелепипеде будет отсутствовать одно измерение и объем параллелепипеда и соответственно смешанное произведение трех векторов, будет равно нулю.
Дата добавления: 2015-09-05; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторное произведение двух векторов | | | Условия взаимного расположения векторов |