Линейные операции над векторами и их свойства

Линейные операции над векторами это операции умножения вектора на число и сложения векторов.

Умножение вектора на число. В результате умножения вектора на число получаем новый вектор 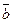, который: коллинеарен вектору ; имеет длину равную произведению длины вектора на модуль числа ; направлен в ту же сторону что и вектор , если и в противоположную сторону, если .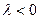

Таким образом, : | | ; ; , .

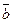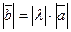Сложение векторов. Суммой двух векторов (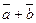) называется вектор, идущий из начала вектора в конец вектора 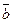при условии, что начало вектора 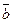, путем параллельного переноса вектора, совмещено с

концом вектора (рис. 1).

Рис. 1

Суммой нескольких векторов ( называется вектор-замыкающая ломаной линии построенной из векторов так, что начало последующего вектора-слагаемого, совмещается с концом предыдущего вектора-слагаемого. Вектор-сумма идет из начала первого вектора- слагаемого в конец последнего вектора-слагаемого (Рис. 2).

Рис. 2

Вычитание векторов – действие обратное сложению векторов. Разностью двух векторов и 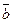называется сумма вектора и вектора, противоположного вектору 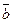, т. е.

.

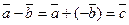Или иначе: разностью двух векторов и 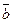называется вектор , который, будучи сложенным с вектором 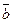, даст вектор (рис. 3).

Рис. 3

Таким образом, всякое выражение в котором векторы складываются или вычитаются можно рассматривать, как векторную сумму.

Основные свойства линейных действий над векторами

1. .

При умножении вектора на число с сомножителями можно работать как в алгебре с числами.

2. | | .

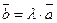
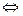
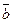Из того, что 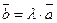следует, что 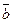| | ; справедливо и обратное, что из обстоятельства 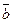| | следует 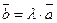, где - единственное число.

3. Переместительный закон сложения векторов (коммутативность):

.

4. Сочетательный закон сложения векторов (ассоциативность):

.

5. Распределительный закон сложения векторов по отношению к действию умножения на число (дистрибутивность):

.

Из рассмотренных свойств следует, что векторную сумму можно преобразовыватьпо тем же правилам, что и обыкновенную алгебраическую сумму: выносить за скобки общий множитель, приводить подобные члены, раскрывать скобки.

Дата добавления: 2015-09-05