Метод Гаусса исключения неизвестных

Две системы линейных алгебраических уравнений называются эквивалентными, если каждое решение первой системыявляется решением второй, и наоборот.

Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:

- перестановка двух уравнений;

-умножение обеих частей одного из уравнений на любое отличное от нуля число;

-прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число.

Элементарные преобразования переводят данную систему уравнений в эквивалентную ей систему.

Используя понятие элементарных преобразований, метод Гаусса позволяет свести систему n уравнений с n неизвестными к ступенчатой эквивалентной треугольной системе, когда первое уравнение содержит все n неизвестных, второе уравнение содержит (n -1) неизвестную, третье – (n -2) неизвестных, и т.д., последнее уравнение содержит одну неизвестную.

Удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу из коэффициентов при неизвестных и свободных членов. Рассмотрим метод Гаусса на примере ранее решенной двумя методами системы.

П р и м е р. Решить методом Гаусса систему:

Р е ш е н и е.

Запишем расширенную матрицу (матрицу коэффициентов и свободных членов), соответствующую решаемой системе, и последовательно преобразуем ее

.

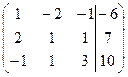
Вторая матрица получена из первой расширенной матрицы системы путем деления каждого уравнения на их коэффициенты при неизвестной (члены первого уравнения делились на 1, второго – на 2, третьего – на -1). Третья матрица получена из второй путем вычитания из элементов второго и третьего уравнений соответствующих элементов первого уравнения. Четвертая матрица получена из третьей матрицы путем деления элементов второй строки (второго уравнения) на 2.5 и деления элементов третьей строки на 1. Пятая матрица получена из четвертой путем вычитания из элементов третьей строки соответствующих элементов второй строки. Пятой матрице соответствует следующая ступенчатая треугольная система

из которой, без затруднения, получаем решение

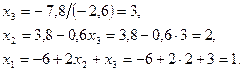
Дата добавления: 2015-09-05