Основные определения. Определителем второго порядка называется число, которое символически записывается в

Определителем второго порядка называется число, которое символически записывается в виде квадратной структуры из четырех элементов (чисел), расположенных в двух строках и двух столбцах:

.

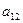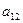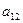Здесь числа , , , - элементы определителя. Читается, например, - a один, два (первый индекс указывает на то в какой строке находится рассматриваемый элемент, второй индекс указывает номер столбца в котором находится рассматриваемый элемент). , - элементы, стоящие на главной диагонали определителя (диагонали, идущей из левого верхнего угла определителя в нижний правый его угол); , - элементы, стоящие на второй (побочной) диагонали определителя. Определитель второго порядка равен разности произведений элементов, стоящих на главной диагонали и на побочной:

.

Определителем третьего порядка называется число, которое символически записывается в виде квадратной структуры из девяти элементов, расположенных в трех строках и трех столбцах и вычисляется по правилу Саррюса

.

Правило Саррюса можно понять из следующих схем, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками:

Аналогично можно дать определение определителей высших порядков, но уже правило вычисления определителя четвертого порядка, типа правила Саррюса, будет трудно понять и запомнить. Позже мы вернемся к вычислению определителей высших порядков. Сейчас же рассмотрим свойства определителей на примере определителей третьего порядка. Эти свойства сохраняют свой вид для определителей любых порядков.

Дата добавления: 2015-09-05