Читайте также:
|
Минором некоторого элемента определителя n- го порядка называется определитель (n-1) -го порядка, получающийся их исходного определителя путем вычеркивания столбца и строки, на пересечении которых находится рассматриваемый элемент.
Алгебраическим дополнением некоторого элемента определителя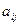 
называется его минор, взятый со своим или противоположным знаком по следующему правилу 
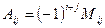, где 
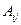- алгебраическое дополнение элемента , 
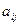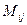- минор этого элемента.
П р и м е р. Для определителя четвертого порядка
найти миноры и алгебраические дополнения элементов 
и 
.
Р е ш е н и е.
, 
,
, 
.
Правило разложения определителя по элементам некоторого ряда: всякий определитель равен сумме произведений элементов некоторого (любого) ряда на их алгебраические дополнения.
Так, например,
+ 
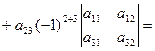
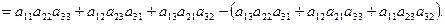
Записано разложение определителя третьего порядка по элементам второй строки. Последняя строка, в приведенных вычислениях, полностью совпадает со значением определителя, вычисленного ранее по правилу Саррюса.
Таким образом, определяя определитель n – го порядка, как квадратную структуру состоящую из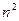 
элементов, расположенных в n столбцах и n строках, сможем вычислять такие определители путем последовательного понижения порядков, разлагая их по элементам того или иного ряда.
П р и м е р.
Для данного определителя 
найти миноры и алгебраические дополнения элементов 
и 
.
Используя свойства определителей, вычислить определитель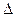 
:
a) разложив его по элементам второй строки;
б) разложив его по элементам третьего столбца;
в) получив предварительно нули во второй строке;
г) получив предварительно нули под главной диагональю.
Р е ш е н и е.
, 
,
, 
.
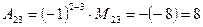а) 
=
.
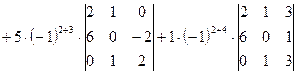б) 
=
.
в) 
.
Последовательно из первого определителя получили второй определитель путем прибавления к элементам второго столбца соответствующих элементов первого столбца умноженных на -3 (получили во втором определителе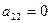 
). Из второго определителя получили третий путем прибавления к элементам третьего столбца соответствующих элементов первого столбца умноженных на -5 (получили в третьем определителе 
). Из третьего определителя получили четвертый путем прибавления к элементам четвертого столбца соответствующих элементов первого столбца домноженных на -1 (получили в четвертом определителе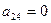 
). Теперь вторая строка определителя содержит три нулевых элемента, и определитель четвертого порядка представляется одним определителем третьего порядка (при разложении по элементам второй строки).
г) 
.
Последовательно из первого определителя получили второй определитель путем перестановки местами первой и второй строки (во втором определителе получили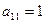 
). Из второго определителя получили третий путем прибавления к элементам второй и третьей строки соответствующих элементов первой строки, предварительно домножив их соответственно на -2 и -6 (получили в третьем определителе 
). Из третьего определителя получили четвертый путем перестановки местами второй и четвертой строк (получили в четвертом определителе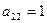 
). Из четвертого пятый определитель получили путем прибавления к элементам третьей и четвертой строк соответствующих элементов второй строки, предварительно помножив их соответственно на 18 и на 5 (получили в пятом определителе 
). Из пятого определителя получили шестой путем вынесения за знак определителя восьмерки - общего для четвертой строки множителя и перестановки местами третьей и четвертой строк (получили в шестом определителе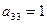 
). Из шестого определителя седьмой получили путем прибавления к элементам четвертой строки соответствующих элементов третьей строки, предварительно домножив их на -25 (получили в седьмом определителе 
). У последнего седьмого определителя под главной диагональю имеем нули, а такой определитель равен произведению элементов стоящих на главной диагонали.
Дата добавления: 2015-09-05; просмотров: 321 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства определителей | | | Основные определения |