Разложение логической функции по переменным

Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма.

Введем обозначение x0=Øx, x1=x. Пусть а - параметр, равный 0 или 1. Тогда xA=1, если x=а, и xA=0, если х¹а.

Теорема. Всякая логическая функция f(x1,., xn) мо-жет быть представлена в следующем виде:

где n ³ m, а дизъюнкция берется по всем 2m наборам значений переменных х1,., хm.

Это равенство называется разложением по переменным х1,., хт. Например, при n=4, m=2 разложение имеет вид:

f(x1, x2, x3, x4)= Øx1 Øx2 f(0, 0, x3, x4) È Øx1 x2 f & (0,1,x3,x4)È x1 Øx2 f(1,0,x3,x4)È x1 x2 f(1,1,x3,x4)

Теорема доказывается подстановкой в обе части равенства произвольного набора всех п переменных.

При m=1 из получаем разложение функции по одной переменной

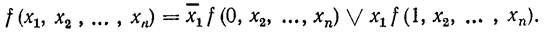
Ясно, что аналогичное разложение справедливо для любой из п переменных. Другой важный случай — разложение по всем п переменным (т=п). При этом все переменные в правой части (3.4) получают фиксированные значения и функции в конъюнкциях правой части становятся равными 0 или 1, что дает:

где дизъюнкция берется по всем наборам на которых f=1. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f. СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице f; каждому единичному набору соответствует конъюнкция всех переменных, в которой Xi взято с отрицанием, если si = 0, и без отрицания, если si = l. Таким образом, существует взаимно однозначное соответствие между таблицей функции f (x1,., хп) и ее СДНФ, и, следовательно, СДНФ для всякой логической функции единственна (точнее, единственна с точностью до порядка букв и конъюнкций: это означает, что ввиду коммутативности дизъюнкции и конъюнкции формулы, получаемые из предыдущей формулы перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Единственная функция, не имеющая СДНФ – это константа 0.

Формулы, содержащие, кроме переменных (и, разумеется, скобок), только знаки функций дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами (напомним, что знак конъюнкции, как правило, опускается). Предыдущая формула приводит к важной теореме.

Теорема. Всякая логическая функция может быть представлена булевой формулой, то есть как суперпозиция конъюнкции, дизъюнкции и отрицания.

Действительно, для всякой функции, кроме константы 0, таким представлением может служить её СДНФ. Константу 0 можно представить булевой формулой Ø xx.

А почему же формула называется “совершенной”? Совершенной называется потому, что она имеет 4 свойства совершенства.

1. В формуле все конъюнкции разные.

2. В конъюнкции все переменные разные.

3. В одной конъюнкции не встречаются переменные вместе с их отрицанием.

4. В конъюнкции столько переменных, сколько в исходной функции f, то есть n. (Число переменных в функции есть ранг этой функции).

Понятие совершенной дизъюнктивной нормальной формы логической функции это такая ДНФ, которая удовлетворяет трём условиям: = в ней нет одинаковых элементарных конъюнкций; =в каждой конъюнкции нет одинаковых пропозициональных букв; =каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке. Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. В ячейках строки́ 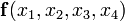отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы.
Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии. Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так:
Пример

x1	x2	x3	φ(x1, x2, x3)
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	1 0 1 0 0 1 1 0

Для построения СДНФ выпишем все наборы, на которых функция равна 1: 000, 010, 101, 110. Для каждого набора построим элементарную конъюнкцию, равную единице на этом наборе: Соединяя эти конъюнкции знаками дизъюнкции, получаем СДНФ заданной функции: Для построения СКНФ выписываем все наборы, на которых функция равна нулю: 001, 011, 100, 111. Для каждого набора построим элементарную дизъюнкцию, равную нулю на этом наборе:

Дата добавления: 2015-09-04