Координатный способ

При этом способе дискретный автомат задается с помощью карты его состояния, которая известна как карта Карно.

Карта Карно содержит 2^m клеток по числу наборов значений переменных. Каждая клетка определяется координатами строк и столбцов, соответствующими определенному набору переменных. Все входные переменные разбиваются на 2 группы так, что одна группа определяет координаты строк, а другая - координаты столбцов. В каждой клетке карты Карно проставляется соответствующее значение функции на заданном наборе. Пример задания функции трех переменных приведен ниже.

Числовое выражение этой функции выглядит так:

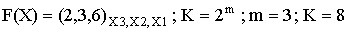
Пример построения карты Карно для функции 4-х переменных. Пусть функция задана в числовой форме и имеет вид:

следовательно, К=16, m=4.

Сначала проводим разметку координат карты Карно без указания значений функции. Для удобства воспользуемся указанием "шапки" в виде прямых линий, “под” которыми переменные входят в значение координат без отрицания. Таким образом, по столбцам и по строкам переменные входят без отрицания в пределах линии-шапки.

Для наглядности координаты клеток карты Карно указаны в трех формах: в виде наборов переменных; в виде двоичного числа, соответствующего порядковому номеру набора переменных; в десятичном эквиваленте номеров наборов переменных. На практике координаты внутри клеток не записывают, в клетках указываются единичные значения функции, соответствующие “координатным” наборам переменных. Нулевые значения функции в клетки можно не записывать, т.е. клетки, координаты которых определяются наборами переменных сулевыми значениями функции, можно оставить пустымулевыми значениями функции, можно оставить пустыми. _________

.

Дата добавления: 2015-09-04