Читайте также:
|
Для всякой логической функции существует соответствующий ей полином Жегалкина и притом только один.
Функция алгебры логики, для которой полином Жегалкина имеет вид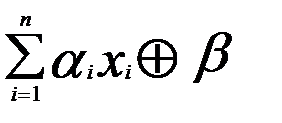 
(здесь знак суммирования означает суммирование по модулю 2, а параметры 
, называется линейной.
Очевидно, что все функции от одной переменной линейны.
Линейными являются, например, функции x 
y и x y 1=x~y.
Для построения полинома Жегалкина можно воспользоваться следующими двумя схемами:
Дата добавления: 2015-09-04; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства операций алгебры Жегалкина | | | Схема 2. |