Матричный способ решения

Обозначим

, , ,

где 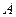- матрица коэффициентов при неизвестных, - матрица-столбец неизвестных, - матрица свободных членов в системе (1.1). Тогда систему (1.1) в матричной форме можно записать в виде

, (1.2)

поскольку

.

Из равенства подчеркнутых матриц в цепи следует система (1.1).

Решение матричной системы (1.2) будет

.

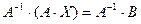
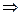
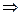
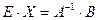
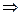
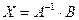Таким образом, матрица неизвестных равна произведению матрицы 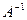- матрице обратной по отношению к матрице коэффициентов 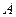на матрицу свободных членов .

П р и м е р. Решим матричным способом (с использованием обратной матрицы) систему ранее решенную методом Крамера:

Р е ш е н и е. Для рассматриваемой системы

, , .

Строим матрицу :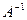

определитель 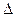, соответствующий матрице 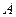, будет

,

алгебраические дополнения элементов определителя 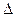, будут

, , ,

, , ,

, , ;

матрица - матрица алгебраических дополнений определителя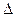

;

матрица

.

П р о в е р к а

,

обратная матрица найдена, верно.

Теперь

= ,

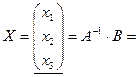
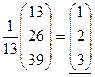из подчеркнутых частей цепи , , .

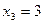Дата добавления: 2015-09-05