Свойства определителей

Сформулируем свойства и проследим их выполнение на числовых примерах.

1. Определитель не изменит своего значения, если в нем строки заменить соответствующими столбцами. Определитель, в котором строки заменены соответствующими столбцами, называется транспонированным по отношению к исходному определителю.

П р и м е р. Пусть исходный определитель

.

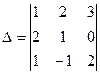Тогда транспонированный определитель

.

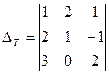Первая строка определителя 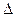стала первым столбцом определителя 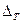. Первый, второй, третий (слева направо) элементы этой первой строки в 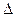стали соответственно первым, вторым, третьим (сверху вниз) элементами первого столбца в 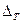. Аналогично строятся второй и третий столбцы определителя 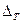. Определитель 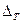получится из определителя 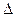, если элементы определителя 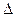повернуть относительно главной диагонали, как вокруг фиксированной оси, на .

, .

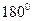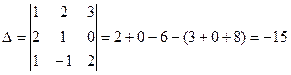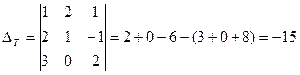Таким образом, на примере показали, что = .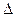

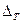Из этого первого свойства следует равноправие строк и столбцов в определителе и впредь мы будем их называть рядами.

2. Если в определителе поменять местами два параллельных ряда, то знак определителя изменится на противоположный, абсолютная величина его не изменится.

П р и м е р.

, .

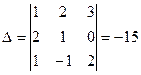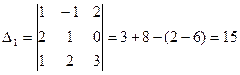В 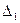по сравнениюс 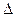мы поменяли местами первый и третий горизонтальные ряды и показали, что = .

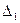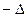С л е д с т в и е. Определитель имеющий два одинаковых параллельных ряда равен нулю.

П р и м е р.

.

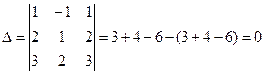3. При умножении определителя на число, на это число можно умножить любой ряд определителя.

П р и м е р.

.

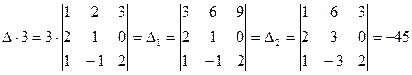В случае 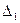на тройку умножили первый горизонтальный ряд определителя 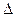, в случае 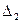умножали на тройку второй вертикальный ряд.

Таким образом, сомножитель общий для элементов некоторого ряда определителя можно выносить за знак определителя.

С л е д с т в и я:

1) определитель, содержащий целый ряд нулей равен нулю;

2) определитель, содержащий два пропорциональных параллельных ряда равен нулю.

4. Если элементы некоторого ряда определителя представлены в виде суммы двух (или большего числа) слагаемых, то исходный определитель можно представить в виде суммы двух (или большего числа) определителей.

П р и м е р.

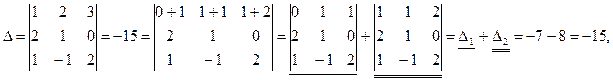где

, .

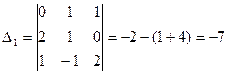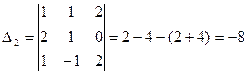С л е д с т в и е.Если к элементам некоторого рядаприбавить соответствующие элементы параллельного ряда, предварительно умножив их на одно и то же число, то значение определителя не изменится.

П р и м е р.

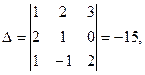
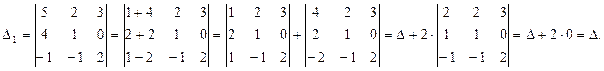Определитель 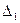получен путем прибавления к элементам первого столбца определителя 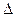соответствующих элементов второго столбца,

помноженных на два.

Дата добавления: 2015-09-05