Читайте также:
|
Вектор вида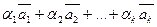 
, где 
(
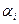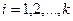) – некоторые числа, называется линейной комбинацией данных векторов 
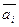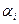. – коэффициенты линейной комбинации. Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам.
Справедливы следующие теоремы
Т е о р е м а 1. Пусть даны два неколлинеарных вектора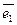 
и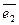 
. Любой компланарный с ними вектор 
раскладывается по ним и такое разложение единственно. Т. е., = 
+ 
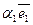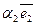, где 
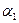и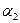 
единственные для этого вектора вполне определенные числа.
Т е о р е м а 2. Пусть даны три некомпланарных вектора 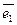, 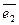и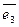 
. Любой вектор раскладывается по ним и такое разложение единственно. Т. е., = + + 
.
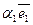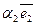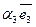Базисом в пространстве называются три некомпланарных вектора, взятых в определенном порядке. Базис позволяет однозначно сопоставить вектору упорядоченную тройку чисел , ,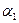 
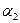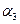- коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если 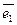, , 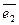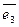- базис и = 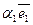+ + 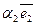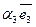, то числа 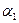, , 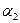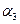называются координатами вектора в данном базисе, при этом пишут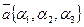 
.
Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты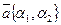 
.
Действия над векторами, заданными своими координатами:
1.При умножении вектора на число все его координаты умножаются
на это число. Т.е.,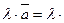 
(
+ + )= 
+ 
+ 
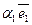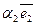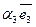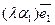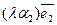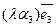и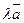 
{ 
, 
, 
}.
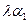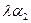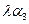2. При сложении векторов складываются их соответствующие координаты. Т. е., если в выбранном базисе ,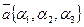 
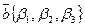, то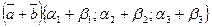 
.
Дата добавления: 2015-09-05; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные операции над векторами и их свойства | | | Аффинные координаты |